2023-2024学年上海市杨浦高级中学高一(上)期中数学试卷
发布:2024/10/2 8:0:1
一、填空题(3'×10=30')
-
1.若指数函数的图像经过点
,则指数函数的解析式为 .(2,14)组卷:661引用:5难度:0.8 -
2.满足{1,2}⊆A⊆{1,2,3,4,5}的集合A有个.
组卷:515引用:13难度:0.7 -
3.关于x的不等式ax2+bx+2>0的解集为{x|-2<x<3},则b的值为 .
组卷:179引用:4难度:0.8 -
4.已知a,b为正数,化简
=.a5b2•(a2b)-1•b3组卷:269引用:4难度:0.7 -
5.已知log189=a,18b=5,则log3645=(用a,b表示).
组卷:3167引用:11难度:0.7 -
6.不等式x2-3>2|x|的解集是
.组卷:44引用:2难度:0.7
三、简答题
-
18.设函数
.y=1|x|-1
(1)在如图平面直角坐标系中画出函数的图像;
(2)试说明函数图象关于y轴对称;
(3)解不等式.1|x|-1>x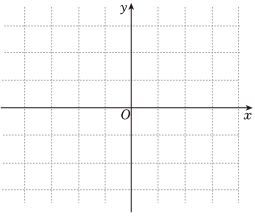 组卷:33引用:1难度:0.5
组卷:33引用:1难度:0.5 -
19.某科研小组对面积为8000平方米的某池塘里的一种生物的生长规律进行研究,一开始在此池塘投放了一定面积的该生物,观察实验得到该生物覆盖面积y(单位:平方米)与所经过月数x(x∈N)的下列数据:
为描述该生物覆盖面积y(单位:平方米)与经过的月数x(x∈N)的关系,现有以下三种函数模型供选择:y=k•ax(k>0,a>1);y=px 0 2 3 4 y 4 25 62.5 156.25 +q(p>0);y=ax2+bx+c.x
(1)试判断哪个函数模型更适合,并求出该模型的函数解析式;
(2)约经过几个月,此生物能覆盖整个池塘?
(3)经过4个月的研究掌握该生物生长规律后,科研小组需改善池塘生态,现有两种方案:
方案一:加入能抑制该生物生长的某种化学物质,使其覆盖面积y与经过的月数x(x≥5)的关系变为y=4•1.7x;
方案二:在4月底集中打捞一次,使其覆盖面积减少到4平方米,生物增长速度不变.
问如何评价这两种方案,并说明理由.组卷:38引用:1难度:0.5


