2022-2023学年山西省运城市教育发展联盟高二（下）期中数学试卷
发布：2024/8/28 10:0:8
一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.
-
1．某班4名同学去参加校运动会3个场馆的志愿者活动，每名同学必须且只能去一个场馆，则不同的选择方法有（ ）
组卷：92引用：3难度：0.8 -
2．在
的展开式中，含x5项的系数为（ ）（x-2x）7组卷：96引用：2难度：0.7 -
3．某校为了研究学生的性别和对待某一活动的态度（支持与不支持）的关系，运用2×2列联表进行独立性检验．整理所得数据后发现，若依据α=0.010的独立性检验，则认为学生性别与是否支持该活动无关；若依据α=0.025的独立性检验，则认为学生性别与是否支持该活动有关，则K2的值可能为（ ）
P（K2≥k0） 0.100 0.050 0.025 0.010 0.001 k0 2.706 3.841 5.024 6.635 10.828 组卷：157引用：4难度：0.9 -
4．下列说法错误的是（ ）
组卷：233引用：5难度：0.8 -
5．已知离散型随机变量X的分布列服从两点分布，且P（X=0）=2-5P（X=1）=a,则a=（ ）
组卷：259引用：3难度：0.8 -
6．设某批产品中，甲、乙、丙三个车间生产的产品分别为50%，30%，20%，甲、乙车间生产的产品的次品率分别为3%，5%，现从中任取一件，若取到的是次品的概率为3.6%，则推测丙车间的次品率为（ ）
组卷：382引用：4难度：0.7 -
7．甲、乙两名高校毕业生准备去北京、上海、广州、杭州、南京、西安六个城市中选择一个城市实习，记事件A为“甲和乙至少一人选择北京”，事件B为“甲和乙选择的城市不同”，则P（B|A）=（ ）
组卷：167引用：2难度：0.9
四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤
-
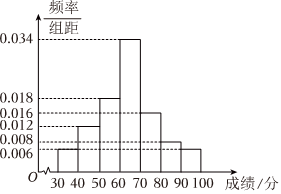21．基础学科招生改革试点，也称强基计划，是教育部开展的招生改革工作，主要是为了选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生．强基计划的校考由试点高校自主命题，校考过程中笔试通过后才能进入面试环节．某省高三2022年有10000名学生报考某试点高校，随机抽取100名学生的笔试成绩，并以此为样本绘制了样本频率分布直方图，如图所示．规定笔试成绩高于70分的学生进入面试环节．
（1）现从该样本中随机抽取两名学生的笔试成绩，求这两名学生中恰有一名学生进入面试环节的概率；
（2）若该省所有报考某试点高校的学生成绩X近似服从正态分布N（μ，σ2），其中σ≈15，μ为样本平均数的估计值（同一组数据用该组区间的中点值作代表），试估计这10000名报考学生中成绩超过94分的学生数（结果四舍五入到整数）．
附参考数据：若随机变量X服从正态分布N（μ，σ2），则P（μ-σ≤X≤μ+σ）≈0.6827，P（μ-2σ≤X≤μ+2σ）≈0.9545，P（μ-3σ≤X≤μ+3σ）≈0.9973．组卷：102引用：2难度：0.6 -
22．某学校开展投篮比赛活动，比赛规则是：每名选手投篮n次（n≥3，n∈N*），每次投篮，若投进，则下一次站在三分线处投篮；若没有投进，则下一次站在两分线处投篮．规定每名选手第一次站在两分线处投篮．站在两分线处投进得2分，否则得0分；站在三分线处投进得3分，否则得0分．已知小明站在两分线处投篮投进的概率为0.6，站在三分线处投篮投进的概率为0.4，且每次投篮相互独立．
（1）记小明前2次投篮累计得分为X，求X的分布列和数学期望；
（2）记第k次投篮时，小明站在三分线处投篮的概率为ak，k=1，2，⋯，n,求ak的表达式．组卷：53引用：2难度：0.6
