当前位置：试卷中心 > 试卷详情

2023-2024学年广西南宁二中高二（上）第一次适应性数学试卷

发布：2024/8/17 4:0:1

一、选择题（本题共8小题，每小题有且仅有一个正确答案，每小题5分，共40分）

1．设集合A={x|x=3k+1，k∈Z}，B={x|x=3k+2，k∈Z}，U为整数集，则∁_U（A∪B）=（　　）
A．{x|x=3k,k∈Z} B．{x|x=3k-1，k∈Z}
C．{x|x=3k-2，k∈Z} D．∅
组卷：3767引用：9难度：0.8
解析
2．设a∈R，（a+i）（1-ai）=2，则a=（　　）
A．-2 B．-1 C．1 D．2
组卷：90引用：5难度：0.8
解析
3．下列函数中，在区间（0，+∞）上单调递增的是（　　）
A．f（x）=-lnx B．
f
（
x
）
=
1
2
x
C．
f
（
x
）
=
-
1
x
D．f（x）=3^|x-1|
组卷：1503引用：22难度：0.7
解析
4．设甲：sin²α+sin²β=1，乙：sinα+cosβ=0，则（　　）
A．甲是乙的充分条件但不是必要条件
B．甲是乙的必要条件但不是充分条件
C．甲是乙的充要条件
D．甲既不是乙的充分条件也不是乙的必要条件
组卷：233引用：7难度：0.7
解析
5．某学校举办作文比赛，共6个主题，每位参赛同学从中随机抽取一个主题准备作文，则甲、乙两位参赛同学抽到不同主题概率为（　　）
A．
5
6
B．
2
3
C．
1
2
D．
1
3
组卷：1955引用：8难度：0.7
解析
6．已知直线l：（m+2）x+（m-1）y+m-1=0，若直线l与连接A（1，-2）、B（2，1）两点的线段总有公共点，则直线l的倾斜角范围为（　　）
A．
[
-
π
4
，
π
4
]
B．
[
3
π
4
，
π
）
C．
[
π
4
，
3
π
4
]
D．
[
0
，
π
4
]
∪
[
3
π
4
，
π
）
组卷：74引用：12难度：0.8
解析
7．向量|
a
|=|
b
|=1，|
c
|=
2
，且
a
+
b
+
c
=
0
，则cos〈
a
-
c
，
b
-
c
〉=（　　）
A．
-
1
5
B．
-
2
5
C．
2
5
D．
4
5
组卷：4035引用：4难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本题共6小题，其中17题10分，其余各题各12分，共70分，解答应写出文字说明、证明过程和验算步骤）

21．在△ABC中，c=2bcosB，
C
=
2
π
3
．
（1）求∠B；
（2）再从条件①、条件②、条件③这三个条件中选择一个作为已知，使△ABC存在且唯一确定，求BC边上中线的长．
条件①：
c
=
2
b
；
条件②：△ABC的周长为
4
+
2
3
；
条件③：△ABC的面积为
3
3
4
．
组卷：230引用：9难度：0.6
解析
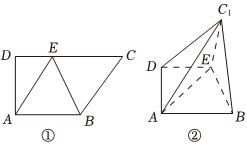22．图①是直角梯形ABCD，AB∥CD，∠D=90°，四边形ABCE是边长为2的菱形，并且∠BCE=60°，以BE为折痕将△BCE折起，使点C到达C₁的位置，且AC₁=
6
．
（1）求证：平面BC₁E⊥平面ABED；
（2）在棱DC₁上是否存在点P，使得点P到平面ABC₁的距离为
15
5
？若存在，求出直线EP与平面ABC₁所成角的正弦值；若不存在，请说明理由．
组卷：516引用：18难度：0.6
解析