2022-2023学年江苏省徐州市高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知复数z满足z（1+i）=5+i,则复数z在复平面内所对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：108引用：4难度：0.8

  解析

• 2．先后两次掷一枚质地均匀的骰子，则两次掷出的点数之和为6的概率为（　　）

  A． 1 9

  B． 5 36

  C． 1 6

  D． 7 36
  组卷：66引用：1难度：0.8

  解析

• 3．已知m,n是两条不重合的直线，α，β是两个不重合的平面，则下列说法正确的是（　　）

  A．若m⊥α，m⊥n,则n⊂α

  B．若m,n与α所成的角相等，则m∥n

  C．若m∥α，m∥β，则α∥β

  D．若m∥n,n⊥β，m⊂α，则α⊥β
  组卷：95引用：2难度：0.7

  解析

• 4．有一组样本数据，x₁，x₂，…，x_n，其平均数为a,中位数为b,方差为c,极差为d.由这组数据得到新样本数据，y₁，y₂，…，y_n，其中y_i=2x_i+8（i=1，2，…，n），则新样本数据的（　　）

  A．样本平均数为2a	B．样本中位数为2b
  C．样本方差为4c	D．样本极差为2d+8
  组卷：108引用：3难度：0.6

  解析

• 5．已知向量

  a

  ，

  b

  的夹角为

  π

  3

  ，若

  （

  a

  -

  b

  ）

  ⊥

  a

  ，则向量

  a

  在向量

  b

  上的投影向量为（　　）

  A． 1 4 b

  B． 1 2 b

  C． 3 2 b

  D． b
  组卷：77引用：2难度：0.7

  解析

• 6．已知

  sin

  （

  α

  +

  π

  3

  ）

  +

  sinα

  =

  3

  3

  ，则

  sin

  （

  2

  α

  -

  π

  6

  ）

  的值是（　　）

  A． 7 9

  B． - 7 9

  C． 2 9

  D． - 2 9
  组卷：355引用：7难度：0.8

  解析

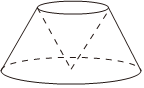• 7．如图，一种工业部件是由一个圆台挖去一个圆锥所制成的．已知圆台的上、下底面半径分别为2和4，且圆台的母线与底面所成的角为

  π

  3

  ，圆锥的底面是圆台的上底面，顶点在圆台的下底面上，则该工业部件的体积为（　　）

  A． 2 3 π

  B． 16 3 π

  C． 7 3 π 3

  D． 56 3 3 π
  组卷：117引用：4难度：0.5

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

• 21．在①

  sin

  A

  cos

  B

  cos

  C

  =

  2

  a

  2

  a

  2

  +

  c

  2

  -

  b

  2

  ，②

  sin

  B

  -

  cos

  B

  =

  2

  b

  -

  a

  c

  ，③△ABC的面积

  S

  =

  2

  4

  b

  （

  bsin

  C

  +

  ctan

  C

  cos

  B

  ）

  这三个条件中任选一个，补充在下面问题中，并完成解答．
  在△ABC中，角A，B，C的对边分别为a,b,c,已知_____．
  （1）求角C；
  （2）若点D在边AB上，且BD=2AD，

  cos

  B

  =

  5

  13

  ，求tan∠BCD．
  注：如果选择多个条件分别解答，按第一个解答计分
  组卷：141引用：5难度：0.5

  解析

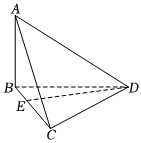• 22．如图，在三棱锥A-BCD中，底面BCD是边长为2的正三角形，AB⊥平面BCD，点E在棱BC上，且BE=λBC，其中0＜λ＜1．
  （1）若二面角A-CD-B为30°，求AB的长；
  （2）若AB=2，求DE与平面ACD所成角的正弦值的取值范围．
  组卷：126引用：1难度：0.6

  解析