当前位置：试卷中心 > 试卷详情

2023-2024学年北京师大附中九年级（上）月考数学试卷（10月份）

发布：2024/9/9 6:0:8

一、选择题。（共20分，每题2分）第1-10题均有四个选项，符合题意的选项均只有一个。

1．抛物线y=（x-3）²+1的顶点坐标是（　　）
A．（-3，1） B．（3，1） C．（-3，-1） D．（3，-1）
组卷：383引用：26难度：0.9
解析
2．用配方法解一元二次方程x²-6x+4=0，配方正确的是（　　）
A．（x+3）²=13 B．（x+3）²=5 C．（x-3）²=13 D．（x-3）²=5
组卷：298引用：8难度：0.7
解析
3．将抛物线y=3x²先向左平移1个单位，再向下平移2个单位，所得抛物线的解析式为（　　）
A．y=3（x-1）²+2 B．y=3（x+1）²-2
C．y=3（x+1）²+2 D．y=3（x-1）²-2
组卷：1145引用：10难度：0.8
解析
4．如图，平面直角坐标系xOy中，A（-4，0），B（0，3），点P为线段AB的中点，则线段OP的长为（　　）
A．
3
2
B．2 C．
5
2
D．5
组卷：629引用：9难度：0.6
解析
5．已知x₁，x₂是一元二次方程x²-2x-1=0的两根，则x₁+x₂-x₁x₂的值是（　　）
A．1 B．3 C．-1 D．-3
组卷：576引用：7难度：0.6
解析
6．关于x的一元二次方程（a-5）x²-4x-1=0有实数根，则a满足（　　）
A．a≥1 B．a＞1且a≠5 C．a≥1且a≠5 D．a≠5
组卷：1466引用：56难度：0.9
解析
7．已知点A（-3，y₁），B（1，y₂），C（4，y₃）在抛物线y=-（x-2）²+5上，则y₁，y₂，y₃的大小关系是（　　）
A．y₁＜y₂＜y₃ B．y₁＜y₃＜y₂ C．y₃＜y₂＜y₁ D．y₃＜y₁＜y₂
组卷：86引用：1难度：0.5
解析
8．函数y=ax²+bx+c（a≠0）中y与自变量x的部分对应值如下表：

x … -1 0 1 2 3 …

y … 8 3 0 -1 0 …

则当y＞8时，x的取值范围是（　　）
A．-1＜x＜5 B．0＜x＜3 C．x＜-1或x＞5 D．x＜0或x＞3
组卷：189引用：2难度：0.5
解析
9．二次函数y=x²-bx+b的图象可能是（　　）
A． B． C． D．
组卷：880引用：6难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题。（共64分，第19题8分，第20题-22题每题6分，第23题8分，第24-25题每题7分，第26-27题每题8分）

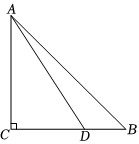26．如图，在△ABC中，AC=BC，∠ACB=90°，点D在BC边上（不与点B，C重合），将线段AD绕点A顺时针旋转90°，得到线段AE，连接DE．
（1）根据题意补全图形，并证明：∠EAC=∠ADC；
（2）取DE的中点F，连接CF，用等式表示线段CF与BD之间的数量关系，并证明．
组卷：73引用：1难度：0.5
解析
27．对于平面图形G₁，G₂和直线y=kx+b（这里k,b均为常数），若它们同时满足以下两个条件：
a.对G₁上任意一点（p,m），均有m≤kp+b；
b.对G₂上任意一点（q,n），均有n≥kq+b.
则称直线y=kx+b是图形G₁，G₂的“分界线”．
回答以下问题．
（1）如图1所示，在平面直角坐标系中有正方形ABCD和三角形EFG．例如：直线y=-x是正方形ABCD和三角形EFG的一条“分界线”．
（i）在下列直线中，可以作为正方形ABCD和三角形EFG的“分界线”的是
（填选项的标号）；
①y=0；
②y=x；
③y=3x；
④y=-x-1．
（ii）若直线y=kx+1是正方形ABCD和三角形EFG的“分界线”，结合图形，求k的取值范围．
（2）如图2所示，在平面直角坐标系中有抛物线M：y=-（x-t）²+2和正方形HIJK，正方形HIJK的顶点H的坐标为（t+2，0）．若直线y=-2x-2是抛物线M和正方形HIJK的“分界线”，直接写出t的取值范围．
组卷：111引用：3难度：0.3
解析