2022-2023学年江苏省苏州市高一（下）期末数学模拟试卷

一、单项选择题：本题共8小题，每小题5分，共40分.

• 1．已知复数z=a+bi（a,b∈R），若

  a

  i

  2023

  +

  2

  =

  b

  +

  i

  ，则

  z

  的虚部是（　　）

  A．-2

  B．-2i

  C．2

  D．2i
  组卷：58引用：2难度：0.8

  解析

• 2．从某班57名同学中选出4人参加户外活动，利用随机数表法抽取样本时，先将57名同学按01，02，…，57进行编号，然后从随机数表第1行的第3列和第4列数字开始往右依次选取两个数字，则选出的第4个同学的编号为（　　）
  

  0347	4373	8636	9647	3661	4698	6371	6297
  7424	6292	4281	1457	2042	5332	3732	1676

  （注：表中的数据为随机数表第1行和第2行）

  A．36

  B．42

  C．46

  D．47
  组卷：143引用：4难度：0.8

  解析

• 3．设m,n是两条不同的直线，α，β是两个不同的平面，则下列结论不正确的是（　　）

  A．若m⊥β，m⊂α，则α⊥β

  B．若m∥α，n⊥α，则m⊥n

  C．若m∥α，m∥β，则α∥β

  D．若m⊂α，n⊂α，m∥β，n∥β，m与n相交，则α∥β
  组卷：117引用：2难度：0.6

  解析

• 4．一组数据按从小到大的顺序排列为2，3，4，x,7，8（其中x≠7），若该组数据的中位数是极差的

  5

  6

  ，则该组数据的60%分位数是（　　）

  A．4

  B．4.5

  C．5

  D．6
  组卷：103引用：4难度：0.7

  解析

• 5．已知

  sin

  （

  4

  π

  3

  -

  α

  ）

  =

  -

  2

  5

  ，则

  cos

  （

  2

  α

  +

  4

  π

  3

  ）

  =（　　）

  A． - 21 25

  B． - 17 25

  C． 17 25

  D． 21 25
  组卷：221引用：2难度：0.7

  解析

• 6．已知事件A，B，且P（A）=0.6，P（B）=0.15，如果A与B互斥，那么P（AB）=p₁，如果A与B相互独立，那么

  P

  （

  A

  B

  ）

  =

  p

  2

  ，则p₁，p₂分别为（　　）

  A．p1=0，p2=0.51	B．p1=0.75，p2=0.51
  C．p1=0，p2=0.45	D．p1=0.75，p2=0.45
  组卷：114引用：1难度：0.8

  解析

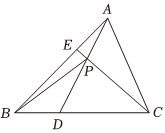• 7．如图，在△ABC中，点D，E分别在边BC和边AB上，D，E分别为BC和BA的三等分点，点D靠近点B，点E靠近点A，AD交CE于点P，设

  BC

  =

  a

  ，

  BA

  =

  b

  ，则

  BP

  =（　　）

  A． - 1 7 a + 3 7 b

  B． 1 7 a + 4 7 b

  C． 1 7 a + 3 7 b

  D． 2 7 a + 4 7 b
  组卷：455引用：5难度：0.6

  解析

四、解答题：本题共6小题，共70分.解答应写出必要的文字说明、证明过程或演算步骤.

• 21．在△ABC中，内角A，B，C的对边分别为a,b,c,且

  b

  sin

  A

  +

  sin

  C

  =

  a

  -

  c

  sin

  B

  +

  c

  sin

  A

  +

  sin

  C

  ．
  （1）求角A的大小；
  （2）若a=2bcosB，a=3，求BC边上中线的长．
  组卷：204引用：3难度：0.5

  解析

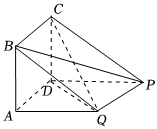• 22．已知直角梯形BQPC中，∠CBQ=90°，BQ∥CP，BC=1，BQ=2，CP=3，A为BQ的中点，CD=

  1

  3

  CP，如图，将四边形ABCD沿AD向上翻折，使科平面ABCD⊥平面ADPQ．
  （1）在PD上是否存在一点H，使得CH∥平面BDQ？
  （2）求二面角B-PQ-C的余弦值．
  组卷：133引用：1难度：0.5

  解析