2022-2023学年福建省龙岩市连城二中等校联考高二(下)期中数学试卷
发布:2024/5/24 8:0:9
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符
-
1.函数f(x)=2x2+1在区间[1,5]上的平均变化率为( )
组卷:51引用:2难度:0.8 -
2.设向量
,e1,e2不共面,已知e3=AB+e1+e2,e3=BC+λe1+e2,e3=4CD+8e1+4e2,若A,C,D三点共线,则λ=( )e3组卷:427引用:6难度:0.8 -
 3.如图,在直三棱柱ABC-A1B1C1中,E为棱A1C1的中点.设=BA,a=BB1,b=BC,则c=( )BE组卷:419引用:6难度:0.9
3.如图,在直三棱柱ABC-A1B1C1中,E为棱A1C1的中点.设=BA,a=BB1,b=BC,则c=( )BE组卷:419引用:6难度:0.9 -
 4.《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑.在鳖臑A-BCD中,AB⊥平面BCD,∠BDC=90°,BD=AB=CD.若建立如图所示的空间直角坐标系,则平面ACD的一个法向量为( )组卷:258引用:1难度:0.8
4.《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑.在鳖臑A-BCD中,AB⊥平面BCD,∠BDC=90°,BD=AB=CD.若建立如图所示的空间直角坐标系,则平面ACD的一个法向量为( )组卷:258引用:1难度:0.8 -
5.现代建筑讲究线条感,曲线之美让人称奇.衡量曲线弯曲程度的重要指标是曲率,曲线的曲率定义如下:若f'(x)是f(x)的导函数,f″(x)是f'(x)的导函数,则曲线y=f(x)在点(x,f(x))处的曲率
.函数f(x)=3lnx的图象在(1,f(1))处的曲率为( )K=|f″(x)|(1+(f′(x))2)32组卷:73引用:7难度:0.7 -
6.已知直线x=a与函数f(x)=x+1,g(x)=ln(2x+1)的图像分别交于A,B两点,则|AB|的最小值为( )
组卷:118引用:3难度:0.5 -
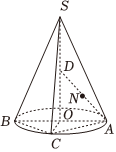 7.如图,在圆锥SO中,AB是底面圆O的直径,SO=AB=4,AC=DC,D为OS的中点,N为AD的中点,则点N到平面SBC的距离为( )组卷:48引用:4难度:0.5
7.如图,在圆锥SO中,AB是底面圆O的直径,SO=AB=4,AC=DC,D为OS的中点,N为AD的中点,则点N到平面SBC的距离为( )组卷:48引用:4难度:0.5
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
-
 21.如图,在三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,且AC=AB1.
21.如图,在三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,且AC=AB1.
(1)证明:AB⊥B1C;
(2)若AC⊥AB1,∠CBB1=,AB=BC,点M在直线AA1上,求直线AB与平面MB1C1所成角的正弦值的最大值.π3组卷:26引用:2难度:0.5 -
22.已知函数f(x)=ln(x+1)+ax(a∈R),g(x)=x3+sinx.
(1)讨论f(x)的单调性;
(2)若a=0,证明:f(x)≤g(x).组卷:62引用:3难度:0.6


