2023-2024学年吉林省长春二中高三(上)第二次调研数学试卷
发布:2024/9/2 5:0:8
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1.已知p:log2x<1,则p的充分不必要条件是( )
组卷:59引用:5难度:0.7 -
2.已知正实数a,b满足
,则(a+1)(b+9)的最小值是( )1a+9b=6组卷:131引用:5难度:0.7 -
3.已知函数f(x)=lg[(a2-1)x2+(a+1)x+1]的值域为R,则实数a的取值范围是( )
组卷:423引用:5难度:0.9 -
4.已知函数f(x)=
,对∀x1,x2∈R,x1≠x2,满足(x1-x2)[f(x1)-f(x2)]>0,则实数a的取值范围是( )ax+1,x≤12x2-(a+1)x+5,x>1组卷:84引用:3难度:0.8 -
5.已知定义在R上的函数f(x)满足f(-x)+f(x)=0,f(x+1)=f(1-x),且当x∈(-1,0)时,f(x)=
(-x),则12-log4=( )f(172)组卷:161引用:3难度:0.8 -
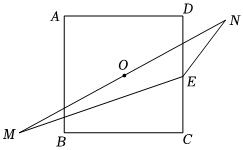 6.如图,在边长为2的正方形ABCD中,其对称中心O平分线段MN,且MN=2BC,点E为DC的中点,则•EM=( )EN组卷:146引用:7难度:0.7
6.如图,在边长为2的正方形ABCD中,其对称中心O平分线段MN,且MN=2BC,点E为DC的中点,则•EM=( )EN组卷:146引用:7难度:0.7 -
7.已知函数f(x)=x2+m与函数
g(x)=-ln1x-3x的图象上至少存在一对关于x轴对称的点,则实数m的取值范围是( )(x∈[12,2])组卷:241引用:7难度:0.7
四、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
-
21.设函数f(x)=ex+asinx+b.
(1)当a=1,x∈[0,+∞)时,f(x)≥0恒成立,求b的范围;
(2)若f(x)在x=0处的切线为x-y-1=0,且方程恰有两解,求实数m的取值范围.f(x)=m-2xx组卷:199引用:5难度:0.3 -
22.已知函数
,f(x)=sinx+x-1ex.x∈[-π,π2]
(1)求证:f(x)在上单调递增;[-π,π2]
(2)当x∈[-π,0]时,[f(x)-sinx]ex-cosx≤ksinx恒成立,求k的取值范围.组卷:59引用:4难度:0.3


