当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省常州外国语学校八年级（上）期中数学试卷

发布：2024/7/26 8:0:9

一、选择题（每题3分，共24分）

1．第24届冬奥会将于2022年在北京和张家口举办．下列四个图分别是第24届冬奥会图标中的一部分，其中是轴对称图形的是（　　）
A． B． C． D．
组卷：325引用：8难度：0.9
解析
2．下列各数中，是无理数的是（　　）
A．
1
7
B．
2
C．0.5 D．
9
组卷：73引用：2难度：0.9
解析
3．下列计算正确的是（　　）
A．
3
2
+
2
=
4
2
B．
5
2
-
3
2
=
5
-
3
C．
18
÷
3
=
6
D．
8
-
3
=
5
组卷：113引用：2难度：0.8
解析
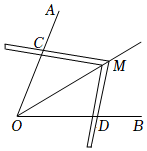4．工人师傅常常利用角尺构造全等三角形的方法来平分一个角．如图，在∠AOB的两边OA、OB上分别在取OC=OD，移动角尺，使角尺两边相同的刻度分别与点C、D重合，这时过角尺顶点M的射线OM就是∠AOB的平分线，这里构造全等三角形的依据是（　　）
A．SSS B．ASA C．AAS D．SAS
组卷：2979引用：33难度：0.7
解析
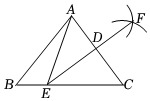5．如图，在△ABC中，点D是AC的中点，分别以点A，C为圆心，大于
1
2
AC的长为半径作弧，两弧交于F，直线FD交BC于点E，连接AE，若AD=2，△ABE的周长为12，则△ABC的周长为（　　）
A．13 B．14 C．15 D．16
组卷：1827引用：15难度：0.6
解析
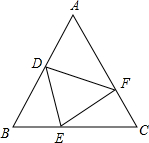6．如图，△ABC中，AB=AC，BD=CE，BE=CF，若∠A=40°，则∠DEF的度数是（　　）
A．75° B．70° C．65° D．60°
组卷：2575引用：6难度：0.9
解析
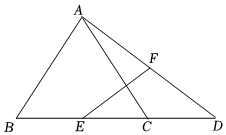7．如图，△ABC中，AB=AC，点D在BC的延长线上，连接AD，点E、F分别是BC、AD的中点，若EF=3，则AD的长为（　　）
A．3 B．3
3
C．3
2
D．6
组卷：215引用：1难度：0.5
解析
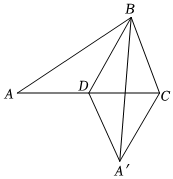8．如图，在△ABC中、D是边AC中点，连接BD，将△ABD沿线段BD翻折后得△A′BD，其中A′C=4，AD=4，AB=
37
，则D到AB边的距离为（　　）
A．
8
111
37
B．
6
111
37
C．
5
111
37
D．
10
111
37
组卷：178引用：1难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（19题20题各8分，21题6分，22题8分，23题6分，24题11分，25题9分）

24．如图1，在△ABC中，AB=AC，D为射线BC上（不与B、C重合）一动点，在AD的右侧射线BC的上方作△ADE，使得AD=AE，∠DAE=∠BAC，连接CE．

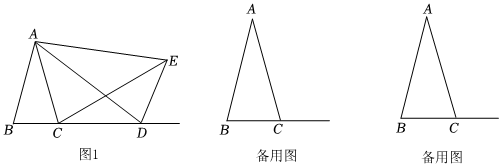
（1）找出图中的一对全等三角形，并证明你的结论；
（2）延长EC交AB的延长线于点F，若∠F=45°，
①利用（1）中的结论求出∠DCE的度数；
②当△ABD是等腰三角形时，直接写出∠ADB的度数；
（3）当D在线段BC上时，若线段BC=3，△ABC面积为3，则四边形ADCE周长的最小值是
．
组卷：570引用：2难度：0.2
解析
25．数与形是数学中的两个最古老，也是最基本的研究对象，它们在一定条件下可以相互转化，数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”可以使复杂问题简单化，抽象问题具体化，从而起到优化解题途径的目的．
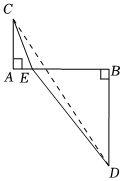
（1）【思想应用】已知m,n均为正实数、且m+n=2，求
m
2
+
1
+
n
2
+
4
的最小值．通过分析，小明想到了利用下面的构造解决此问题：如图，AB=2，AC=1，BD=2，AC⊥AB，BD⊥AB，点E是线段AB上的动点，且不与端点重合，连接CE，DE，设AE=m,BE=n.
①用含m的代数式表示CE=
，用含n的代数式表示DE=
；
②据此写出
m
2
+
1
+
n
2
+
4
的最小值
；
（2）【类比应用】根据上述的方法，代数式
x
2
+
25
+
（
x
-
16
）
2
+
49
的最小值是
；
（3）【拓展应用】
①已知a,b,c为正数，且a+b+c=1，试运用构图法，画出图形，并写出
a
2
+
b
2
+
b
2
+
c
2
+
c
2
+
a
2
的最小值；
②若a,b为正数，写出以
a
2
+
b
2
，
4
a
2
+
b
2
，
a
2
+
4
b
2
为边的三角形的面积
．
组卷：564引用：2难度：0.2
解析