2023-2024学年安徽省安庆市怀宁县新安中学高二（上）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分。

• 1．已知空间A、B、C、D四点共面，且其中任意三点均不共线，设P为空间中任意一点，若

  BD

  =

  5

  PA

  -

  4

  PB

  +

  λ

  PC

  ，则λ=（　　）

  A．2

  B．-2

  C．1

  D．-1
  组卷：99引用：4难度：0.5

  解析

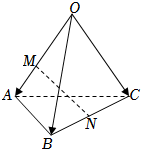• 2．如图，空间四边形OABC中，OA=OB=OC=2，∠AOC=∠BOC=

  π

  2

  ．∠AOB=

  π

  3

  ，点M，N分别在OA，BC上，且OM=2MA，BN=CN，则MN=（　　）

  A． 22 3

  B． 46 3

  C． 34 3

  D． 21 3
  组卷：74引用：3难度：0.6

  解析

• 3．圆x²+y²+2x+4y-3=0上到直线x+y+1=0的距离为

  2

  的点有（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：732引用：19难度：0.7

  解析

• 4．设直线l：3x+2y-6=0，P（m,n）为直线l上动点，则m²+n²-2n的最小值为（　　）

  A． - 4 13

  B． 3 13

  C． 3 13 13

  D． 13 13
  组卷：60引用：2难度：0.8

  解析

• 5．直线x+y-1=0与直线x-2y-4=0交于点P，则点P到直线kx-y+1+2k=0（k∈R）的最大距离为（　　）

  A． 2

  B．2

  C． 2 5

  D．4
  组卷：450引用：8难度：0.7

  解析

• 6．在平面直角坐标系中，已知点A（-1，0），B（2，0），圆

  C

  ：

  （

  x

  -

  2

  ）

  2

  +

  （

  y

  -

  m

  ）

  2

  =

  1

  4

  （

  m

  ＞

  0

  ）

  ，在圆上存在点P满足|PA|=2|PB|，则实数m的取值范围是（　　）

  A． [ 2 2 ， 6 2 ]

  B． [ 5 4 ， 21 2 ]

  C． （ 0 ， 21 2 ]

  D． [ 5 2 ， 21 2 ]
  组卷：402引用：10难度：0.5

  解析

• 7．过定点A的直线x-my=0（m∈R）与过定点B的直线mx+y-m+3=0（m∈R）交于点P（x,y），则|PA|²+|PB|²的值为（　　）

  A． 10

  B．10

  C．2 5

  D．20
  组卷：196引用：4难度：0.7

  解析

四、解答题（70分）

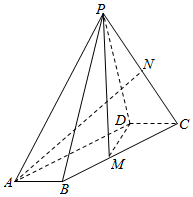• 21．如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠ABC=120°，AB=1，BC=4，PA=

  15

  ，M，N分别为BC，PC的中点，PD⊥DC，PM⊥MD．
  （Ⅰ）证明：AB⊥PM；
  （Ⅱ）求直线AN与平面PDM所成角的正弦值．
  组卷：6769引用：22难度：0.4

  解析

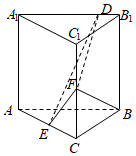• 22．已知直三棱柱ABC-A₁B₁C₁中，侧面AA₁B₁B为正方形，AB=BC=2，E，F分别为AC和CC₁的中点，D为棱A₁B₁上的点，BF⊥A₁B₁．
  （1）证明：BF⊥DE；
  （2）当B₁D为何值时，面BB₁C₁C与面DFE所成的二面角的正弦值最小？
  组卷：9816引用：49难度：0.5

  解析