当前位置：试卷中心 > 试卷详情

2022-2023学年四川省达州中学联盟七年级（下）期中数学试卷

发布：2024/7/12 8:0:9

一、选择题（本大题共10个小题，每小题4分，共40分，每小题均有四个选项，其中只有一项符合题目要求）

1．如果一个角的补角是130°，那么这个角的余角的度数是（　　）
A．30° B．40° C．50° D．90°
组卷：385引用：6难度：0.9
解析
2．已知m、n是正整数，且a^m=3，aⁿ=2，则a^m+n的值为（　　）
A．5 B．1 C．6 D．
2
3
组卷：810引用：7难度：0.9
解析
3．下列各式中能用平方差公式计算的是（　　）
A．（a+3b）（3a-b） B．（3a-b）（3a-b）
C．（3a-b）（-3a+b） D．（3a-b）（3a+b）
组卷：415引用：5难度：0.7
解析
4．某蓄水池的横断面示意图如图所示，分深水区和浅水区，如果以固定的流量把水蓄满蓄水池，下面的图象能大致表示水的深度h和注水时间t之间关系的是（　　）
A． B． C． D．
组卷：1785引用：19难度：0.9
解析
5．下列计算中正确的是（　　）
A．（-aⁿ）²=aⁿ⁺² B．（-a³）⁴=（-a⁴）³
C．（a⁴）⁴=a⁴•a⁴ D．（a⁴）⁴=（a²）⁸
组卷：107引用：2难度：0.9
解析
6．如图，平行线AB、CD被直线EF所截，过点B作BG⊥EF于点G，已知∠1=50°，则∠B=（　　）
A．20° B．30° C．40° D．50°
组卷：869引用：18难度：0.7
解析
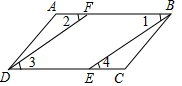7．如图，点F，E分别在线段AB和CD上，下列条件能判定AB∥CD的是（　　）
A．∠1=∠2 B．∠1=∠4 C．∠4=∠2 D．∠3=∠4
组卷：1336引用：23难度：0.9
解析
8．给出下列说法：
①从直线外一点到这条直线的垂线段叫做这个点到这条直线的距离；
②三角形的角平分线是射线；
③三角形的高所在的直线交于一点，这一点不在三角形内就在三角形外；
④任何一个三角形都有三条高、三条中线、三条角平分线；
⑤三角形的三条角平分线交于一点，且这点在三角形内．
正确的说法有（　　）
A．1个 B．2个 C．3个 D．4个
组卷：1027引用：2难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共10小题，共90分）

24．阅读下列材料：利用完全平方公式，将多项式x²+bx+c变形为（x+m）²+n的形式，然后由（x+m）²≥0就可求出多项式x²+bx+c的最小值．
例题：求多项式x²-4x+5的最小值．
解：x²-4x+5=x²-4x+4+1=（x-2）²+1，
因为（x-2）²≥0，所以（x-2）²+1≥1．
当x=2时，（x-2）²+1=1．因此（x-2）²+1有最小值，最小值为1，即x²-4x+5的最小值为1．
通过阅读，理解材料的解题思路，请解决以下问题：
（1）【理解探究】
已知代数式A=x²+10x+20，则A的最小值为
；
（2）【类比应用】
张大爷家有甲、乙两块长方形菜地，已知甲菜地的两边长分别是（3a+2）米、（2a+5）米，乙菜地的两边长分别是5a米、（a+5）米，试比较这两块菜地的面积S_甲和S_乙的大小，并说明理由；
（3）【拓展升华】
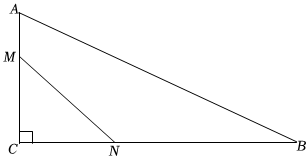
如图，△ABC中，∠C=90°，AC=5cm,BC=10cm,点M、N分别是线段AC和BC上的动点，点M从A点出发以1cm/s的速度向C点运动；同时点N从C点出发以2cm/s的速度向B点运动，当其中一点到达终点时，两点同时停止运动，设运动的时间为t,则当t的值为多少时，△MCN的面积最大，最大值为多少？
组卷：468引用：8难度：0.3
解析
25．如图1，AB∥CD，EF与直线AB，CD相交，点P为直线AB、CD之间的一点．
（1）若
∠
AEP
=
1
4
∠
AEF
，
∠
CFP
=
1
4
∠
CFE
，求∠P 的度数；
（2）如图2，在（1）的条件下，EM平分∠PEF交PF于点M，FN平分∠PFE交PE于点N，猜想∠EMF+∠ENF的结果，并证明你的结论；
（3）如图3，在（1）的条件下，点K是射线EA上一动点，作射线PK并在射线PK上取一点G，使得PG=PE，再作∠GPF的平分线交直线GE于点Q，则当K点在射线EA上移动时，∠PQG的大小是否变化？若不变，请求出∠PQG的大小；若变化，请求出其变化范围．
组卷：55引用：1难度：0.5
解析