2022-2023学年四川省达州市达川区万家初级中学八年级（上）期末数学试卷

一、选择题（每小题3分，共30分）

• 1．在给出的一组数0，π，

  5

  ，3.14，

  3

  9

  ，

  22

  7

  中，无理数有（　　）

  A．1个

  B．2个

  C．3个

  D．5个
  组卷：2754引用：57难度：0.9

  解析

• 2．甲、乙、丙、丁四人进行射击测试，每人10次射击成绩平均数均是9.2环，方差分别为S_甲²=0.56，S_乙²=0.60，S_丙²=0.50，S_丁²=0.45，则成绩最稳定的是（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  组卷：2095引用：134难度：0.9

  解析

• 3．下列四组数，分别以各组数中的三个数据为边长构建三角形，不能组成直角三角形的一组是（　　）

  A．7，24，25

  B．12，16，20

  C．4，6，8

  D．3，4，5
  组卷：180引用：2难度：0.9

  解析

• 4．下列等式成立的是（　　）

  A．3+4 2 =7 2

  B． 3 × 2 = 5

  C． 3 ÷ 1 6 =2 3

  D． （ - 3 ） 2 =3
  组卷：1468引用：30难度：0.7

  解析

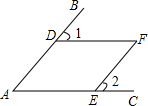• 5．如图，AC∥DF，AB∥EF，点D、E分别在AB、AC上，若∠2=50°，则∠1的大小是（　　）

  A．30°

  B．40°

  C．50°

  D．60°
  组卷：781引用：80难度：0.9

  解析

• 6．已知代数式与-3x^m-1y³与

  5

  2

  xⁿy^m+n是同类项，那么m、n的值分别是（　　）

  A． m = 2 n = - 1

  B． m = - 2 n = - 1

  C． m = 2 n = 1

  D． m = - 2 n = 1
  组卷：208引用：1难度：0.8

  解析

• 7．如图，一棵大树（树干与地面垂直）在一次强台风中于离地面6米B处折断倒下，倒下后的树顶C与树根A的距离为8米，则这棵大树在折断前的高度为（　　）

  A．10米

  B．12米

  C．14米

  D．16米
  组卷：1720引用：11难度：0.7

  解析

• 8．下列四点中，在函数y=3x+2的图象上的点是（　　）

  A．（-1，1）

  B．（-1，-1）

  C．（2，0）

  D．（0，-1.5）
  组卷：2023引用：27难度：0.9

  解析

三、解答题（共72分）

• 24．阅读理解：已知实数x,y满足3x-y=5…①，2x+3y=7…②，求x-4y和7x+5y的值．仔细观察两个方程未知数的系数之间的关系，本题可以通过适当变形整体求得代数式的值，如由①-②可得x-4y=-2，由①+②×2可得7x+5y=19．这样的解题思想就是通常所说的“整体思想”．利用“整体思想”，解决下列问题：
  （1）已知二元一次方程组

  2 x + y = 7

  x + 2 y = 8

  ，则x-y=

  ，x+y=

  ；
  （2）买20支铅笔、3块橡皮、2本日记本共需32元，买39支铅笔、5块橡皮、3本日记本共需58元，求购买5支铅笔、5块橡皮5本日记本共需多少元？
  （3）对于实数x,y,定义新运算：x*y=ax+by+c,其中a,b,c是常数，等式右边是实数运算．已知3*5=15，4*7=28，求1*1的值．
  组卷：3923引用：29难度：0.5

  解析

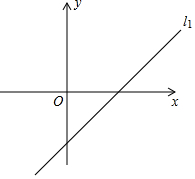• 25．表格中的两组对应值满足一次函数y=kx+b,函数图象为直线l₁，如图所示．将函数y=kx+b中的k与b交换位置后得一次函数y=bx+k,其图象为直线l₂.设直线l₁交y轴于点A，直线l₁交直线l₂于点B，直线l₂交y轴于点C．
  

  x	-2	4
  y	-4	2

  （1）求直线l₂的解析式；
  （2）若点P在直线l₁上，且△BCP的面积是△ABC的面积的（1+

  2

  ）倍，求点P的坐标；
  （3）若直线y=a分别与直线l₁，l₂及y轴的三个交点中，其中一点是另两点所成线段的中点，求a的值．
  组卷：576引用：2难度：0.3

  解析