2022-2023学年江苏省苏州市高新实验中学八年级(上)月考数学试卷(12月份)
发布:2024/9/7 12:0:8
一、选择题(本大题共10小题,每小题2分,共20分)
-
1.下列图案不是轴对称图形的是( )
组卷:85引用:6难度:0.7 -
2.下列各组数中,以它们为边长的线段能构成直角三角形的是( )
组卷:102引用:4难度:0.6 -
3.用四舍五入法得到的近似数1.05万,下列说法正确的是( )
组卷:365引用:3难度:0.8 -
4.一次函数y=-3x-2的图象不经过( )
组卷:908引用:84难度:0.9 -
5.给出下列四个说法:①一个数的平方等于1,那么这个数就是1;②4是8的算术平方根;③平方根等于它本身的数只有0;④8的立方根是±2.其中,正确的是( )
组卷:2353引用:12难度:0.8 -
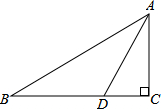 6.如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为( )5组卷:18674引用:61难度:0.9
6.如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为( )5组卷:18674引用:61难度:0.9 -
7.规定:[k,b]是一次函数y=kx+b(k、b为实数,k≠0)的“特征数”,若“特征数”是[4,-m]的一次函数是正比例函数,则点(2-m,2+m)所在的象限是( )
组卷:354引用:3难度:0.7 -
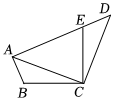 8.如图在四边形ABCD中,点E在边AD上,∠BCE=∠ACD,∠BAC=∠D=40°,AB=DE,AC=AE,则∠B的度数为( )组卷:38引用:1难度:0.6
8.如图在四边形ABCD中,点E在边AD上,∠BCE=∠ACD,∠BAC=∠D=40°,AB=DE,AC=AE,则∠B的度数为( )组卷:38引用:1难度:0.6 -
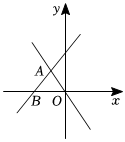 9.如图,已知一次函数y=kx+b的图象经过点A(-1,2)和点B(-2,0),一次函数y=mx的图象经过点A,则关于x的不等式组0<kx+b<mx的解集为( )组卷:1526引用:2难度:0.6
9.如图,已知一次函数y=kx+b的图象经过点A(-1,2)和点B(-2,0),一次函数y=mx的图象经过点A,则关于x的不等式组0<kx+b<mx的解集为( )组卷:1526引用:2难度:0.6
三、解答题(本大题共10小题,共56分)
-
27.定义:对于一次函数y1=ax+b、y2=cx+d,我们称函数y=m(ax+b)+n(cx+d)(ma+nc≠0)为函数y1、y2的“组合函数”.
(1)若m=3,n=1,试判断函数y=5x+2是否为函数y1=x+1、y2=2x-1的“组合函数”,并说明理由;
(2)设函数y1=x-p-2与y2=-x+3p的图象相交于点P.
①若m+n>1,点P在函数y1、y2的“组合函数”图象的上方,求p的取值范围;
②若p≠1,函数y1、y2的“组合函数”图象经过点P.是否存在大小确定的m值,对于不等于1的任意实数p,都有“组合函数”图象与x轴交点Q的位置不变?若存在,请求出m的值及此时点Q的坐标;若不存在,请说明理由.组卷:3493引用:5难度:0.1 -
28.如图1,在Rt△ABC中,∠ACB=90°,动点M从点A出发沿A-C-B向点B匀速运动,动点N从点B出发沿B-C-A向点A运动.设MC的长为y1(cm),NC的长为y2(cm),点M的运动时间为x(s),y1、y2与x的函数图象如图2所示.
(1)线段AC=cm,点M运动s后点N开始运动;
(2)求点P的坐标,并写出它的实际意义;
(3)当∠CMN=45°时,求x的值.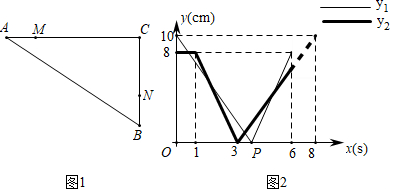 组卷:459引用:2难度:0.3
组卷:459引用:2难度:0.3


