2023年广东省深圳市宝安中学（集团）中考数学三模试卷
发布：2024/5/24 8:0:9
一.选择题（共10小题，满分30分，每小题3分）
-
1．2023的相反数的倒数是（ ）
组卷：351引用：12难度：0.9 -
2．下列食品标识中，既是轴对称图形又是中心对称图形的是（ ）
组卷：434引用：9难度：0.9 -
3．已知点P（2x+6，x-4）在第四象限，则实数x的取值范围在数轴上表示正确的为（ ）
组卷：2068引用：16难度：0.7 -
4．每年的6月6日是全国爱眼日，就在手机充斥着人们生活，占用大部分时间的同时，其蓝光危害以及用眼过度带来的影响也在悄然的威胁着人们的视力健康，某班为了解全班学生的视力情况，随机抽取了10名学生进行调查，将抽取学生的视力统计结果如下表．下列说法错误的是（ ）
视力 4.5 4.6 4.7 4.8 4.9 5.0 人数 1 1 2 3 1 2 组卷：138引用：4难度：0.7 -
5．下列计算正确的是（ ）
组卷：79引用：1难度：0.7 -
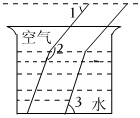6．光线在不同介质中的传播速度是不同的，因此当光线从水中射向空气时要发生折射，由于折射率相同，所以在水中平行的光线，在空气中也是平行的，如图，若∠1=50°，∠2=158°，则∠3的度数为（ ）组卷：293引用：3难度：0.7 -
7．下列命题中真命题的个数是（ ）
①在同一平面内，过一点有且只有一条直线与已知直线平行；
②过一点有且只有一条直线与已知直线垂直；
③顺次连接菱形各边中点所得到的四边形是矩形；
④平分弦的直径垂直于弦；
⑤三角形的内心到三角形三边的距离相等．组卷：250引用：2难度：0.7
三.解答题（共7小题，满分55分）
-
21．如图①，已知线段AB与直线l,过A、B两点，作⊙O使其与直线l相切，切点为P，易证∠APB=∠AHB＞∠AQB，可知点P对线段AB的视角最大．
问题提出
（1）如图②，已知△ABP的外接圆为⊙O，PQ与⊙O相切于点P，交AB的延长线于点Q．
①请判断∠BPQ与∠A的大小关系，并说明理由．
②若QB=2，AB=6，求PQ的长．
问题解决
（2）如图③，一大型游乐场入口AB设在道路DN边上，在“雪亮工程”中，为了加强安全管理，结合现实情况，相关部门准备在与地面道路DN夹角为60°的射线DM方向上（位于垂直于地面的平面内）确定一个位置C，并架设斜杆AC，在斜杆AC的中点P处安装一摄像头，对入口AB实施监控（其中点A、B、D、P、C、M、N在同一平面内），已知DA=40米，AB=25米，调研发现，当∠APB最大时监控效果最好，请问在射线DM上是否存在一点C，使得∠APB达到最大？若存在，请确定点C在DM上的位置及斜杆AC的长度；若不存在，请说明理由．
组卷：1170引用：2难度：0.3 -
22．（1）【探究发现】如图①，已知四边形ABCD是正方形，点E为CD边上一点（不与端点重合），连接BE，作点D关于BE的对称点D，DD的延长线与BC的延长线交于点F，连接 BD'，D′E．
①小明探究发现：当点E在CD上移动时，△BCE≌△DCF．并给出如下不完整的证明过程，请帮他补充完整．
证明：延长BE交DF于点G．
②进一步探究发现，当点 D'与点F重合时，∠CDF=．
（2）【类比迁移】如图②，四边形ABCD为矩形，点E为CD边上一点，连接BE，作点D关于BE的对称点D，DD'的延长线与BC的延长线交于点F，连接BD，CD，DE．当CD⊥DF，AB=2，BC=3时，求CD′的长；
（3）【拓展应用】如图③，已知四边形ABCD为菱形，，AC=4，点F为线段BD上一动点，AD=23
将线段AD绕点A按顺时针方向旋转，当点D旋转后的对应点E落在菱形的边上（顶点除外）时，如果DF=EF，请直接写出此时OF的长．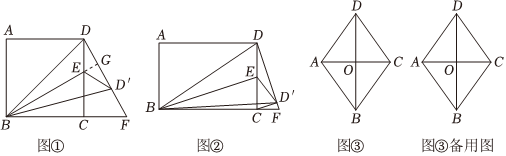
组卷：537引用：1难度：0.1
