2020-2021学年江苏省无锡市惠山区八校联考九年级（上）月考数学试卷（12月份）
发布：2024/8/7 8:0:9
一、选择题（本大题共有10小题，每小题3分，共30分，在每小题所给出的四个选项中，只有一项是正确的，请把正确选项前的字母代号填在题后的括号内）
-
1．sin60°=（ ）
组卷：290引用：27难度：0.9 -
2．若△ABC∽△DEF，相似比为1：2，则△ABC与△DEF的周长比为（ ）
组卷：351引用：16难度：0.7 -
3．下列方程中，没有实数根的是（ ）
组卷：1650引用：28难度：0.9 -
4．已知⊙O的半径为3，若OP=4，则点P与⊙O的位置关系是（ ）
组卷：299引用：5难度：0.9 -
5．下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（ ）甲 乙 丙 丁 平均数（cm） 180 185 185 180 方差 3.6 3.6 7.4 8.1 组卷：1034引用：27难度：0.9 -
6．下列说法正确的是（ ）
组卷：758引用：8难度：0.9 -
7．某人沿着坡度为1：2.4的斜坡向上前进了130m,那么他的高度上升了（ ）
组卷：736引用：12难度：0.7 -
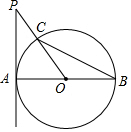8．如图，AB是⊙O的直径，直线PA与⊙O相切于点A，PO交⊙O于点C，连接BC．若∠P=50°，则∠ABC的度数为（ ）组卷：1319引用：12难度：0.7 -
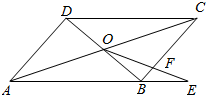9．如图，▱ABCD对角线AC与BD交于点O，且AD=3，AB=5，在AB延长线上取一点E，使BE=AB，连接OE交BC于F，则BF的长为（ ）25组卷：2141引用：17难度：0.6
三、解答题（本大题共10小题，共84分，解答时应写出文字说明、证明过程或演算步骤）
-
27．如果三角形的两个内角α与β满足2α+β=90°，那么我们称这样的三角形为“准互余三角形”．
（1）若△ABC是“准互余三角形”，∠C＞90°，∠A=60°，则∠B=°；
（2）如图①，在Rt△ABC中，∠ACB=90°，AC=4，BC=5．若AD是∠BAC的平分线，不难证明△ABD是“准互余三角形”．试问在边BC上是否存在点E（异于点D），使得△ABE也是“准互余三角形”？若存在，请求出BE的长；若不存在，请说明理由．
（3）如图②，在四边形ABCD中，AB=7，CD=12，BD⊥CD，∠ABD=2∠BCD，且△ABC是“准互余三角形”，求对角线AC的长．
组卷：4223引用：15难度：0.1 -
28．【发现问题】爱好数学的小明在做作业时碰到这样的一道题目：
如图①，点O为坐标原点，⊙O的半径为1，点A（2，0）．动点B在⊙O上，连接AB，作等边△ABC（A，B，C为顺时针顺序），求OC的最大值
【解决问题】小明经过多次的尝试与探索，终于得到解题思路：在图①中，连接OB，以OB为边在OB的左侧作等边三角形BOE，连接AE．
（1）请你找出图中与OC相等的线段，并说明理由；
（2）线段OC的最大值为．
【灵活运用】
（3）如图②，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA=2，PM=PB，∠BPM=90°，求线段AM长的最大值及此时点P的坐标．
【迁移拓展】
（4）如图③，BC=4，点D是以BC为直径的半圆上不同于B、C的一个动点，以BD为边作等边△ABD，请直接写出AC的最值．2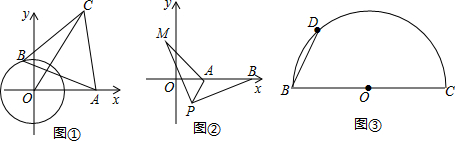
组卷：2083引用：8难度：0.1
