人教A版（2019）选择性必修第一册《第一章 空间向量与立体几何》2023年单元测试卷（4）

一、选择题

• 1．空间四边形ABCD中，M、G分别是BC、CD的中点，则

  MG

  -

  AB

  +

  AD

  等于（　　）

  A． 3 2 DB

  B．3 MG

  C．3 GM

  D．2 MG
  组卷：174引用：7难度：0.9

  解析

• 2．若直线l的方向向量为

  a

  =

  （

  1

  ，

  0

  ，

  2

  ）

  ，平面α的法向量为

  n

  =（-2，0，-4），则（　　）

  A．l∥α

  B．l⊥α

  C．l⊂α

  D．l与α斜交
  组卷：676引用：28难度：0.7

  解析

• 3．以下命题中，不正确的个数为（　　）
  ①|

  a

  |-|

  b

  |=|

  a

  +

  b

  |是

  a

  ，

  b

  共线的充要条件；
  ②若

  a

  ∥

  b

  ，则存在唯一的实数λ，使

  a

  =λ

  b

  ；
  ③若

  a

  •

  b

  =0，

  b

  •

  c

  =0，则

  a

  =

  c

  ；
  ④若{

  a

  ，

  b

  ，

  c

  }为空间的一个基底，则{

  a

  +

  b

  ，

  b

  +

  c

  ，

  c

  +

  a

  }构成空间的另一个基底；
  ⑤|（

  a

  •

  b

  ）•

  c

  |=|

  a

  |•|

  b

  |•|

  c

  |．

  A．2

  B．3

  C．4

  D．5
  组卷：113引用：7难度：0.9

  解析

• 4．若向量

  a

  =（1，λ，2），

  b

  =（2，-1，2），且

  a

  与

  b

  的夹角余弦值为

  8

  9

  ，则λ等于（　　）

  A．2

  B．-2

  C．-2或 2 55

  D．2或- 2 55
  组卷：443引用：64难度：0.9

  解析

• 5．空间四边形OABC中，OB=OC，∠AOB=∠AOC=

  π

  3

  ，则cos＜

  OA

  ，

  BC

  ＞的值是（　　）

  A． 1 2

  B． 2 2

  C．- 1 2

  D．0
  组卷：169引用：29难度：0.9

  解析

• 6．平行六面体ABCD-A₁B₁C₁D₁中，若

  A

  C

  1

  =

  x

  AB

  +

  2

  y

  BC

  -

  3

  z

  C

  C

  1

  ，则x+y+z=（　　）

  A．1

  B． 7 6

  C． 5 6

  D． 2 3
  组卷：307引用：4难度：0.8

  解析

三、解答题

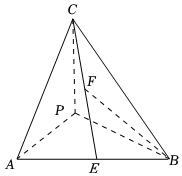• 19．如图，四面体P-ABC中，PA、PB、PC两两垂直，PA=PB=2，PC=4，E是AB的中点，F是CE的中点．
  （1）建立适当的直角坐标系，写出点B、C、E、F的坐标；
  （2）求EF与底面ABP所成角的余弦值．
  组卷：46引用：2难度：0.3

  解析

• 20．已知ABCD为正方形，PD⊥平面ABCD，PD=AD=2，
  （1）求异面直线PC与BD所成角的余弦值；
  （2）求PC与平面PBD所成角的余弦值；
  （3）设M为BC的中点，在线段PB上是否存在一点E，使PC⊥面ADE？若存在，确定E点位置；若不存在，说明理由．
  组卷：85引用：2难度：0.3

  解析