2023-2024学年贵州省九年级（上）质量测评数学试卷（一）

一、选择题：以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请在答题卡相应位置作答，每小题3分，共36分。

• 1．下列方程中，是关于x的一元二次方程的是（　　）

  A．2x=7

  B．x2+y=5

  C． x = 1 x + 1

  D．x2+x=4
  组卷：565引用：17难度：0.8

  解析

• 2．如图，▱ABCD中，对角线AC，BD相交于点O，OA=3，若要使平行四边形ABCD为矩形，则OB的长度为（　　）

  A．4

  B．3

  C．2

  D．1
  组卷：1279引用：15难度：0.9

  解析

• 3．一元二次方程5x²-2x+2=0的一次项系数是（　　）

  A．5

  B．-2

  C．2

  D．0
  组卷：645引用：13难度：0.8

  解析

• 4．下列平行四边形中，根据图中所标出的数据，不一定是菱形的是（　　）

  A．

  B．

  C．

  D．
  组卷：1998引用：22难度：0.8

  解析

• 5．解方程4x²-9=0最适当的方法是（　　）

  A．直接开方法

  B．配方法

  C．公式法

  D．分解因式法
  组卷：63引用：1难度：0.7

  解析

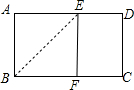• 6．如图，将长方形纸片折叠，使A点落在BC上的F处，折痕为BE，若沿EF剪下，则折叠部分是一个正方形，其数学原理是（　　）

  A．邻边相等的矩形是正方形

  B．对角线相等的菱形是正方形

  C．两个全等的直角三角形构成正方形

  D．轴对称图形是正方形
  组卷：1574引用：29难度：0.9

  解析

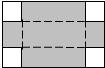• 7．如图是一张长8cm、宽5cm的矩形纸板，将纸板四个角各剪去一个同样的正方形，可制成底面积是18cm²的一个无盖长方体纸盒，设剪去的正方形边长为x cm,那么x满足的方程是（　　）

  A．40-4x2=18	B．（8-2x）（5-2x）=18
  C．40-2（8x+5x）=18	D．（8-2x）（5-2x）=9
  组卷：1292引用：21难度：0.9

  解析

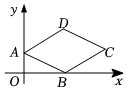• 8．如图，在菱形ABCD中，点B在x轴上，点C的坐标为（6，2），点A的坐标为（0，2），则点D的坐标为（　　）

  A．（4，4）

  B．（3，3）

  C．（3，4）

  D．（2，3）
  组卷：299引用：6难度：0.5

  解析

三、解答题：本大题共9小题，共98分。解答应写出必要的文字说明、证明过程或演算步骤。

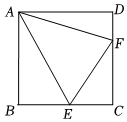• 24．如图，Rt△CEF中，∠C=90°，∠CEF，∠CFE外角平分线交于点A，过点A分别作直线CE，CF的垂线，B，D为垂足．
  （1）∠EAF=

  °（直接写出结果不写解答过程）；
  （2）①求证：四边形ABCD是正方形．
  ②若BE=EC=3，求DF的长．
  组卷：1286引用：6难度：0.5

  解析

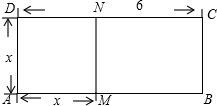• 25．我们知道：x²-6x=（x²-6x+9）-9=（x-3）²-9；-x²+10=-（x²-10x+25）+25=-（x-5）²+25，这一种方法称为配方法，利用配方法请解以下各题：
  （1）按上面材料提示的方法填空：a²-4a=

  =

  ．-a²+12a=

  =

  ．
  （2）探究：当a取不同的实数时在得到的代数式a²-4a的值中是否存在最小值？请说明理由．
  （3）应用：如图．已知线段AB=6，M是AB上的一个动点，设AM=x,以AM为一边作正方形AMND，再以MB、MN为一组邻边作长方形MBCN．问：当点M在AB上运动时，长方形MBCN的面积是否存在最大值？若存在，请求出这个最大值；否则请说明理由．
  组卷：714引用：25难度：0.7

  解析