2022-2023学年黑龙江省齐齐哈尔市龙沙区八年级（下）期末数学试卷

一、单选题（每题3分，共30分）

• 1．下列式子一定是二次根式是（　　）

  A． - 4

  B．π

  C． 3 a

  D． 7
  组卷：185引用：3难度：0.9

  解析

• 2．计算：

  -

  2

  ×

  7

  =（　　）

  A． 14

  B． - 14

  C． 2 7

  D． - 2 7
  组卷：170引用：4难度：0.8

  解析

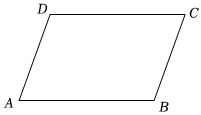• 3．如图，在平行四边形ABCD中，若∠B=2∠A，则∠C的度数为（　　）

  A．60°

  B．45°

  C．120°

  D．135°
  组卷：178引用：4难度：0.7

  解析

• 4．下列函数是正比例函数的是（　　）

  A． y = x 3

  B． y = 3 x

  C．y=x2+1

  D．y=3x+1
  组卷：494引用：3难度：0.8

  解析

• 5．一组数据：3，4，5，6，6的中位数是（　　）

  A．4

  B．4.5

  C．5

  D．6
  组卷：20引用：1难度：0.8

  解析

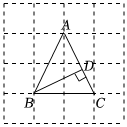• 6．如图，网格中的每个小正方形的边长为1，△ABC的顶点A、B、C均在网格的格点上，BD⊥AC于点D，则BD的长为（　　）

  A． 2 5 3

  B． 4 5 5

  C． 3 5 4

  D． 3 5 5
  组卷：227引用：1难度：0.5

  解析

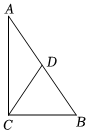• 7．如图，在△ABC中，∠ACB=90°，AB=10，点D为斜边AB上的中点，则CD为（　　）

  A．10

  B．3

  C．5

  D．4
  组卷：258引用：6难度：0.5

  解析

• 8．一组数据的方差为S²，如果把这组数据中的每个数据都扩大为原来的3倍，那么所得到的一组新数据的方差为（　　）

  A． S 2 3

  B．S2

  C．3S2

  D．9S2
  组卷：426引用：4难度：0.5

  解析

三、解答题（共60分）

• 25．【课本再现】
  （1）如图1，正方形ABCD的对角线相交于点O，点O又是正方形A₁B₁C₁O的一个顶点，而且这两个正方形的边长都为1，四边形OEBF为两个正方形重叠部分．正方形A₁B₁C₁O可绕点O转动．则下列结论正确的是

  （填序号即可）．
  ①△AEO≌△BFO；
  ②OE=OF；
  ③四边形OEBF的面积总等于

  1

  4

  S

  正方形

  ABCD

  ；
  ④连接EF，总有AE²+CF²=EF²．
  【类比迁移】
  （2）如图2，矩形ABCD的中心O是矩形A₁B₁C₁O的一个顶点，A₁O与边AB相交于点E，C₁O与边CB相交于点F，连接EF，矩形A₁B₁C₁O可绕着点O旋转，猜想AE，CF，EF之间的数量关系，并进行证明；
  【拓展应用】
  （3）如图3，在Rt△ACB中，∠C=90°，AC=3cm,BC=4cm,直角∠EDF的顶点D在边AB的中点处，它的两条边DE和DF分别与直线AC，BC相交于点E，F，∠EDF可绕着点D旋转，当AE=2cm时，求线段EF的长度．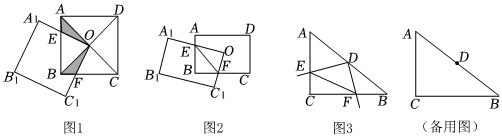
  
  组卷：506引用：8难度：0.5

  解析

• 26．综合与探索
  【探索发现】如图1，等腰直角三角形ABC中，∠ACB=90°，CB=CA，过点A作AD⊥l交于点D，过点B作BE⊥l交于点E，易得△ADC≌△CEB，我们称这种全等模型为“k型全等”．（不需要证明）
  【迁移应用】如图2，在直角坐标系中，直线l₁：y=2x+4分别与y轴，x轴交于点A、B，
  （1）直接写出OA=

  ，OB=

  ；
  （2）在第二象限构造等腰直角△ABE，使得∠BAE=90°，则点E的坐标为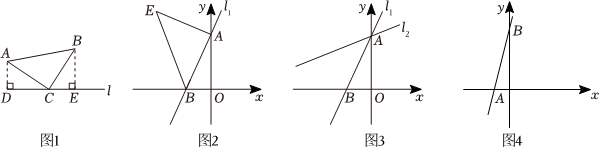

  ；
  
  （3）如图3，将直线l₁绕点A顺时针旋转45°得到l₂，求l₂的函数表达式；
  【拓展应用】
  （4）如图4，直线AB：y=2x+8分别交x轴和y轴于A，B两点，点C在第二象限内一点，在平面内是否存在一点D，使以A、B、C、D为顶点的四边形为正方形？若存在，请直接写出点D的坐标；若不存在，请说明理由．
  组卷：1068引用：4难度：0.5

  解析