2023年广东省东莞市翰林实验学校中考数学三模试卷

一、选择题（本大题共10小题，每小题3分，共30分）

• 1．-2021的倒数是（　　）

  A．2021

  B． 1 2021

  C．-2021

  D． - 1 2021
  组卷：1151引用：144难度：0.8

  解析

• 2．若a＞b,下列不等式不一定成立的是（　　）

  A．a-5＞b-5

  B．-5a＜-5b

  C． a c ＞ b c

  D．a+c＞b+c
  组卷：1948引用：27难度：0.8

  解析

• 3．若代数式

  x

  x

  -

  1

  有意义，则实数x的取值范围是（　　）

  A．x≠1

  B．x≥0

  C．x＞0

  D．x≥0且x≠1
  组卷：2238引用：126难度：0.9

  解析

• 4．下列运算正确的是（　　）

  A．x4+x2=x6	B．x2•x3=x6
  C．（x2）3=x6	D．x2-y2=（x-y）2
  组卷：922引用：11难度：0.9

  解析

• 5．某小区14户家庭的日用电量统计如下表：

  日用电量	3	4	5	6	7	8
  户数	1	6	3	2	1	1

  这14户家庭日用电量的众数、中位数分别是（　　）

  A．4，4.5

  B．4，5.5

  C．6，1.5

  D．1，1.5
  组卷：180引用：6难度：0.6

  解析

• 6．某种病毒直径是0.00000012米，数字0.00000012用科学记数法表示为（　　）

  A．0.12×10-7

  B．0.12×10-6

  C．1.2×10-7

  D．12×10-6
  组卷：405引用：8难度：0.9

  解析

• 7．将抛物线

  y

  =

  1

  2

  x

  2

  +

  5

  向左平移2个单位后，得到新抛物线的解析式是（　　）

  A． y = 1 2 （ x + 2 ） 2 + 5	B． y = 1 2 （ x - 2 ） 2 + 5
  C． y = 1 2 x 2 + 3	D． y = 1 2 x 2 + 7
  组卷：386引用：4难度：0.6

  解析

五、解答题（本大题共2小题，每题12分，共24分）

• 22．如图①，在正方形ABCD中，点E是CD上一动点，将正方形沿着BE折叠，点C落在点F处，连接BE，CF，延长CF交AD于点G．
  
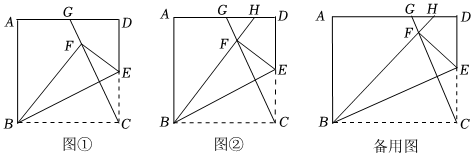
  （1）求证：△BCE≌△CDG．
  （2）如图②，在（1）的条件下，延长BF交AD于点H．
  ①求证：HG=HF；
  ②若

  HD

  HF

  =

  4

  5

  ，CE=9，求线段DE的长．
  （3）将正方形改成矩形，同样沿着BE折叠，连接CF，延长CF，BF交直线AD于G，H两点，若

  AB

  BC

  =k,

  HD

  HF

  =

  4

  5

  ，则

  DE

  EC

  =

  ．（用含k的代数式表示）．
  组卷：277引用：4难度：0.5

  解析

• 23．如图，已知抛物线y=x²+bx+c与x轴相交于A（-1，0），B（m,0）两点，与y轴相交于点C（0，-3），抛物线的顶点为D．
  （1）求抛物线的解析式；
  （2）若点E在x轴上，且∠ECB=∠CBD，求点E的坐标．
  （3）若P是直线BC下方抛物线上任意一点，过点P作PH⊥x轴于点H，与BC交于点M．
  ①求线段PM长度的最大值．
  ②在①的条件下，若F为y轴上一动点，求PH+HF+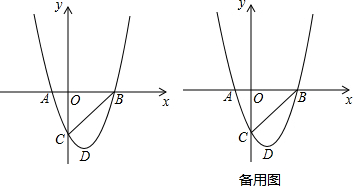

  2

  2

  CF的最小值．
  
  组卷：2771引用：8难度：0.1

  解析