2022-2023学年福建省三明市高一(下)期末数学试卷
发布:2024/6/12 8:0:8
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知i为虚数单位,若z•(1+i)=2i,则|z|=( )
组卷:83引用:8难度:0.9 -
2.已知圆锥底面半径为1,高为2,则该圆锥侧面积为( )
组卷:97引用:4难度:0.7 -
3.已知平面向量
,a满足|b|=|a|=1,b⊥(aa),则-2b与a的夹角为( )b组卷:82引用:2难度:0.7 -
4.一次投篮练习后体育老师统计了第一小组10个同学的命中次数作为样本,计算出他们的平均命中次数为6,方差为3,后来这个小组又增加了一个同学,投篮命中次数为6,那么这个小组11个同学投篮命中次数组成的新样本的方差是( )
组卷:85引用:2难度:0.8 -
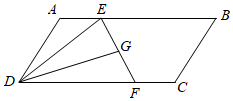 5.如图,在平行四边形ABCD中,为EF的中点,则AE=13AB,CF=13CD,G=( )DG组卷:1205引用:7难度:0.5
5.如图,在平行四边形ABCD中,为EF的中点,则AE=13AB,CF=13CD,G=( )DG组卷:1205引用:7难度:0.5 -
6.设α,β是两个不同的平面,l,m是两条不同的直线,则下列命题中正确的是( )
组卷:86引用:3难度:0.7 -
7.麒麟山位于三明市区中部,海拔262米,原名牛垄山.在地名普查时,发现山腰有一块“孔子戏麒麟”石碑,故更现名.山顶的麒麟阁仿古塔造型是八角重檐阁.小李为测量麒麟阁的高度选取了与底部水平的直线AC,如图,测得∠DAC=30°,∠DBC=45°,AB=18米,则麒麟阁的高度CD约为(参考数据:
,2≈1.414)( )3=1.732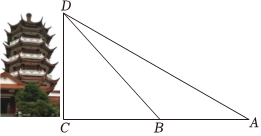 组卷:47引用:2难度:0.6
组卷:47引用:2难度:0.6
四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
-
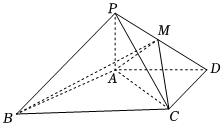 21.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2,BC=4,PA=.2
21.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2,BC=4,PA=.2
(1)求证:AB⊥PC;
(2)在线段PD上是否存在一点M,使得BM与平面ABCD所成角的正切值为,若存在,求二面角M-AC-D的大小,若不存在,请说明理由.2626组卷:94引用:1难度:0.5 -
22.已知△ABC的内角A,B,C的对边分别为a,b,c.点D在BC上,且
.AD=2
(1)若sin∠ADC=2sinB,求c;
(2)若AD是∠BAC的角平分线,且,求△ABC周长的最小值.∠BAC=2π3组卷:90引用:2难度:0.6


