2022-2023学年浙江省宁波市奉化区高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知向量

  a

  =

  （

  2

  ，

  3

  ）

  ，

  b

  =

  （

  -

  1

  ，-

  2

  ）

  ，则

  2

  a

  -

  b

  =（　　）

  A．（3，5）

  B．（-5，-7）

  C．（5，8）

  D．（3，4）
  组卷：129引用：4难度：0.7

  解析

• 2．复数z=ai+b（a,b∈R）是纯虚数的充分不必要条件是（　　）

  A．a≠0且b=0

  B．b=0

  C．a=1且b=0

  D．a=b=0
  组卷：173引用：6难度：0.7

  解析

• 3．水平放置的△ABC有一边在水平线上，它的斜二测直观图是边长为2的正△A′B′C′，则△ABC的面积是（　　）

  A． 3

  B． 2 3

  C． 6

  D． 2 6
  组卷：65引用：2难度：0.7

  解析

• 4．某市场供应的电子产品中，甲厂产品的合格率是90%，乙厂产品的合格率是80%．若从该市场供应的电子产品中任意购买甲、乙厂各一件电子产品，则该产品都不是合格品的概率为（　　）

  A．2%

  B．30%

  C．72%

  D．26%
  组卷：398引用：3难度：0.7

  解析

• 5．设m,n是不同的直线，α，β是不同的平面，则下列命题正确的是（　　）

  A．若m⊥n,n∥α，则m⊥α	B．若m∥β，β⊥α，则m⊥α
  C．若m⊥α，α⊥β，则m∥β	D．若m⊥α，m⊥β，则α∥β
  组卷：269引用：14难度：0.7

  解析

• 6．若数据x₁+m、x₂+m、⋯、x_n+m的平均数是5，方差是4，数据3x₁+1、3x₂+1、⋯、3x_n+1的平均数是10，标准差是s,则下列结论正确的是（　　）

  A．m=2，s=6

  B．m=2，s=36

  C．m=4，s=6

  D．m=4，s=36
  组卷：370引用：4难度：0.8

  解析

• 7．在锐角△ABC中，角A，B，C的对边分别为a,b,c,且满足c-b=2bcosA．若λsinA-cos（C-B）＜2恒成立，则实数λ的取值范围为（　　）

  A． （ - ∞ ， 2 2 ]

  B． （ - ∞ ， 2 2 ）

  C． （ - ∞ ， 5 3 3 ]

  D． （ - ∞ ， 5 3 3 ）
  组卷：289引用：11难度：0.4

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．如图，为测量鼓浪郑成功雕像AB的高度及景点C与F之间的距离（B，C，D，F在同一水平面善个，雕像垂直该水平面于点B，且B，C，D三点共线），某校研究性学习小组同学在C，D，F三点处测得顶点A的仰角分别为45°，30°，30°，若∠FCB=60°，CD=16（

  3

  -1）米
  （1）求雕像AB高度；
  （2）求景点C与F之间的距离．
  组卷：158引用：6难度：0.3

  解析

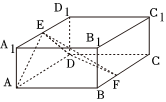• 22．如图，直四棱柱ABCD-A₁B₁C₁D₁的底面ABCD是菱形，E是A₁D₁的中点，F为线段BC上一点，AB=2，AA₁=1，∠BAD=60°．
  （1）证明：当BF=FC时，D₁F∥平面AEB；
  （2）若

  BF

  =

  1

  4

  BC

  ，求二面角A-DE-F的余弦值为

  ．
  组卷：119引用：1难度：0.4

  解析