当前位置：试卷中心 > 试卷详情

2023-2024学年江西省宜春市丰城九中28、29班高三（上）开学数学试卷

发布：2024/8/29 1:0:9

一、单项选择题：本题共8个小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．复数z满足（z+1）i=1-i,则z的共轭复数的虚部是（　　）
A．1 B．-1 C．i D．-i
组卷：52引用：8难度：0.8
解析
2．已知集合A={x|4^x-2^x+1＜0}，B={x|y=lg（x+1）}，则A∩（∁_RB）=（　　）
A．（-∞，-1] B．（-∞，1） C．（-1，1） D．（0，1）
组卷：23引用：3难度：0.8
解析
3．已知平面向量
a
=
（
2
5
5
，
5
5
）
，
b
为单位向量，且
（
a
+
2
b
）
⊥
（
a
-
b
）
，则向量
b
在向量
a
上的投影向量的坐标为（　　）
A．
（
-
2
5
5
，-
5
5
）
B．
（
2
5
5
，
5
5
）
C．
（
2
5
5
，-
5
5
）
D．
（
-
2
5
5
，
5
5
）
组卷：24引用：1难度：0.8
解析
4．设函数
f
（
x
）
=
2
x
2
-
ax
•
lg
x
-
1
x
+
1
为奇函数，则实数a的值为（　　）
A．-1 B．0 C．1 D．2
组卷：128引用：4难度：0.6
解析
5．已知A（0，-2），B（2，0），点P为圆x²+y²-2x-8y+13=0上任意一点，则△PAB面积的最大值为（　　）
A．5 B．
5
-
2
2
C．
5
2
D．
5
+
2
2
组卷：342引用：4难度：0.5
解析
6．在四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD是矩形，且AB=3，AD=4，PA=
4
3
5
，则二面角P-BD-A的大小为（　　）
A．30° B．45° C．60° D．75°
组卷：156引用：8难度：0.4
解析
7．已知正项数列{a_n}中，
a
1
=
2
，
a
n
+
1
=
2
a
n
+
3
×
5
n
，则数列{a_n}的通项a_n=（　　）
A．-3×2^n-1 B．3×2^n-1 C．5ⁿ+3×2^n-1 D．5ⁿ-3×2^n-1
组卷：259引用：3难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

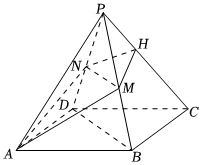21．已知四棱锥P-ABCD，底面ABCD为菱形，PD=PB，H为PC上的点，过AH的平面分别交PB，PD于点M，N，且BD∥平面AMHN．
（1）证明：MN⊥PC；
（2）当H为PC的中点，
PA
=
PC
=
3
AB
，PA与平面ABCD所成的角为60°，求平面PAM与平面AMN所成的锐二面角的余弦值．
组卷：208引用：12难度：0.6
解析
22．已知函数f（x）=lnx-mx²+（1-2m）x+1．
（1）若m=1，求f（x）的极值；
（2）若对任意x＞0，f（x）≤0恒成立，求整数m的最小值．
组卷：620引用：13难度：0.6
解析