当前位置：试卷中心 > 试卷详情

2022-2023学年广西河池市东兰县八年级（下）期末数学试卷

发布：2024/7/5 8:0:9

一．选择题（共12小题，满分36分，每小题3分）

1．使二次根式
x
-
2
有意义的x的取值范围是（　　）
A．x＞0 B．x＞2 C．x≥2 D．x≠2
组卷：2335引用：23难度：0.9
解析
2．下列各曲线中，表示y是x的函数的有（　　）
A．1个 B．2个 C．3个 D．4个
组卷：950引用：5难度：0.7
解析
3．下列各组数中，不能作为直角三角形三边长的是（　　）
A．0.3，0.4，0.5 B．12，16，20
C．1，
2
，
3
D．11，40，41
组卷：414引用：8难度：0.6
解析
4．一家鞋店在一段时间内销售了某款运动鞋30双，该款的各种尺码鞋销售量如图所示．鞋店决定在下一次进货时增加一些尺码为23.5cm的该款运动鞋，影响鞋店这一决策的统计量是（　　）
A．平均数 B．中位数 C．众数 D．方差
组卷：719引用：15难度：0.5
解析
5．下列运算正确的是（　　）
A．
5
+
3
=
8
B．
12
-
3
=
2
3
C．
3
×
2
=6 D．
3
÷
1
3
=3
组卷：2409引用：14难度：0.7
解析
6．把两块形状大小完全相同的含有45°角的三角板的一边拼在一起，则所得到的图形不可能有（　　）
A．正方形
B．等边三角形
C．等腰直角三角形
D．平行四边形（非矩形、菱形、正方形）
组卷：207引用：4难度：0.9
解析
7．人体生命活动所需能量主要由食物中的糖类提供．如图是小潘早餐后一段时间内血糖浓度变化曲线图．下列描述正确的是（　　）
A．从9时至10时血糖呈下降状态
B．10时血糖最高
C．从10时至12时血糖呈上升状态
D．这段时间有3个时刻血糖浓度达到7.0mmol•L^-1
组卷：73引用：4难度：0.7
解析
8．如图，矩形ABCD中，对角线AC，BD交于点O．若∠AOB=60°，BD=6，则AB的长为（　　）
A．4 B．4
3
C．3 D．5
组卷：526引用：7难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三．解答题（共8小题，满分0分）

25．问题提出：

（1）如图①，在等边三角形ABC中，AB=4，AD为BC边上的高，点E为AC的中点，连接BE交AD于点O，则AO的长为
；
问题探究：
（2）如图②，在正方形ABCD中，AB=6，点P为正方形内一点，当
S
△
ABP
=
1
4
S
正方形
ABCD
时，求PA+PB的最小值；
问题解决：
（3）如图③，四边形ABCD是某现代农业生态园部分平面示意图，其中AB∥CD，∠C=90°，∠A=60°，AB=AD，CD=300米，△ABD的中心O是一座有机蔬菜餐厅，生态园的入口M是CD上的中点，BM是一条有机蔬菜展览走廊，BC是一条循环生态河，现需要在BC边上取点E，BM上找点P，修建道路ME、EP、OP，为了节省成本需要修建的道路最短，即ME+EP+OP的值最小；是否存在这样的点E、P，使得ME+EP+OP的值最小？若存在请求出ME+EP+OP的最小值；若不存在，请说明理由．
组卷：738引用：7难度：0.5
解析
26．在数学实践活动课上，“卓越”小组准备研究如下问题：如图，EF为直尺的一条边，四边形ABCD为一正方形纸板（∠DAB、∠ABC、∠BCD、∠D均为直角）
（1）【操作发现】
如图①小组成员小方把正方形的一条边AB与EF重合放置，刘老师在与同学们交流研讨时又做出了∠DAF的平分线AQ，交正方形的边于点P．
则此时∠PAB的度数为
；∠PAB与∠DAE的度数之间的关系为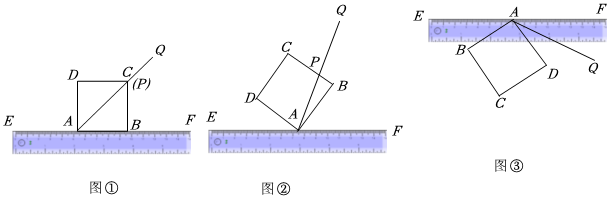
．

（2）【问题探究】
受小方同学的启发，小组成员小丽将正方形纸板按如图②放置，若此时记∠DAE的度数为α，其他条件不变，请帮小丽同学探究：∠PAB与∠DAE的度数之间的关系是否发生改变，并说明理由．
（3）【拓展延伸】
组内其他同学也都继续探索，将正方形按如图③放置，刘老师同样做出了∠DAF的平分线AQ，请直接写出∠QAB与∠DAE的度数之间的关系．
组卷：715引用：7难度：0.6
解析