2023年T8联盟高考数学压轴试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．纯洁的冰雪，激情的约会，2030年冬奥会预计在印度孟买举行．按常理，该次冬奥会共有7个大项，如冰球、冰壶、滑冰、滑雪、雪车等；一个大项又包含多个小项，如滑冰又分为花样滑冰、短道速滑、速度滑冰三个小项．若集合U代表所有项目的集合，一个大项看作是几个小项组成的集合，其中集合A为滑冰三个小项构成的集合，下列说法不正确的是（　　）

  A．“短道速滑”不属于集合A相对于全集U的补集

  B．“雪车”与“滑雪”交集为空集

  C．“速度滑冰”与“冰壶”交集不为空集

  D．集合U包含“滑冰”
  组卷：347引用：5难度：0.8

  解析

• 2．若复数z满足z（1+i）²=1-i,则

  z

  的虚部为（　　）

  A． - 1 2 i

  B． - 1 2

  C． 1 2 i

  D． 1 2
  组卷：52引用：4难度：0.8

  解析

• 3．已知函数f（x）=|sinπx|，

  g

  （

  x

  ）

  =

  sin

  π

  2

  x

  ，若函数φ（x）=f（x），x∈{x|f（x）≠g（x）}，则φ（x）的最小正周期为（　　）

  A．π

  B．2

  C．4

  D．4π
  组卷：44引用：3难度：0.7

  解析

• 4．设F₁，A分别是椭圆

  x

  2

  16

  +

  y

  2

  7

  =

  1

  的左焦点和右顶点，点P为椭圆上异于A点的任意一点，则使得

  P

  F

  1

  •

  PA

  =

  0

  成立的点P的个数为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：114引用：3难度：0.7

  解析

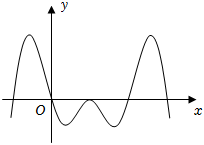• 5．已知函数f（x）的部分图象如图所示，则f（x）的解析式可能为（　　）

  A．f（x）=xcosπx	B．f（x）=（x-1）sinπx
  C．f（x）=xcos[π（x+1）]	D．f（x）=（x-1）cosπx
  组卷：104引用：6难度：0.7

  解析

• 6．已知正数a,b,c满足2022^a=2023，2023^b=2022，c=ln2，下列说法正确的是（　　）

  A．logac＞logbc	B．logca＞logcb
  C．ac＜bc	D．ca＜cb
  组卷：132引用：3难度：0.6

  解析

• 7．已知抛物线

  C

  1

  ：

  y

  =

  x

  2

  +

  2

  x

  和

  C

  2

  ：

  y

  =

  -

  x

  2

  +

  a

  ，若C₁和C₂有且仅有两条公切线l₁和l₂，l₁和C₁、C₂分别相切于M，N点，l₂与C₁、C₂分别相切于P，Q两点，则线段PQ与MN（　　）

  A．总是互相垂直	B．总是互相平分
  C．总是互相垂直且平分	D．上述说法均不正确
  组卷：62引用：3难度：0.6

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤

• 21．已知椭圆

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0），四点P₁（-2，1），

  P

  2

  （

  0

  ，

  2

  ）

  ，P₃（2，1），P₄（3，1）中恰有三点在椭圆C上．
  （1）求椭圆C的方程；
  （2）椭圆C上是否存在异于P2的两点M，N使得直线P₂M与P₂N的斜率之和与直线MN的斜率（不为零）的2倍互为相反数？若存在，请判断直线MN是否过定点；若不存在，请说明理由．
  组卷：272引用：4难度：0.5

  解析

• 22．已知

  f

  （

  x

  ）

  =

  2

  x

  -

  sinx

  -

  a

  lnx

  ．
  （1）当a=1时，讨论函数f（x）的极值点个数；
  （2）若存在x₁，x₂（0＜x₁＜x₂），使f（x₁）=f（x₂），求证：x₁x₂＜a.
  组卷：132引用：5难度：0.5

  解析