2022-2023学年上海市虹口区民办新复兴中学九年级（上）期中数学试卷

一、选择题（本大题共6题，每题4分，共24分）

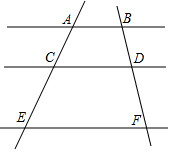• 1．如图，已知AB∥CD∥EF，BD：DF=1：2，那么下列结论正确的是（　　）

  A．AC：AE=1：3

  B．CE：EA=1：3

  C．CD：EF=1：2

  D．AB：CD=1：2
  组卷：761引用：11难度：0.9

  解析

• 2．下列命题中，说法正确的是（　　）

  A．所有菱形都相似

  B．两边对应成比例且有一组角对应相等的两个三角形相似

  C．三角形的重心到一个顶点的距离，等于它到这个顶点对边距离的两倍

  D．斜边和直角边对应成比例，两个直角三角形相似
  组卷：235引用：6难度：0.6

  解析

• 3．如果函数y=kx+b的图象经过第一、二、四象限，那么函数y=kx²+b的大致图象是（　　）

  A．

  B．

  C．

  D．
  组卷：22引用：2难度：0.5

  解析

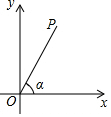• 4．如图，直角坐标平面内有一点P（2，4），那么OP与x轴正半轴的夹角α的余切值为（　　）

  A．2

  B． 1 2

  C． 5 5

  D． 5
  组卷：432引用：4难度：0.8

  解析

• 5．若

  a

  =2

  e

  ，向量

  b

  和向量

  a

  方向相反，且|

  b

  |=2|

  a

  |，则下列结论中不正确的是（　　）

  A．| a |=2

  B．| b |=4

  C． b =4 e

  D． a = - 1 2 b
  组卷：305引用：4难度：0.7

  解析

• 6．若⊙O所在平面内一点P到⊙O上的点的最大距离为a,最小距离为b（a＞b），则此圆的半径为（　　）

  A． a + b 2

  B． a - b 2

  C． a + b 2 或 a - b 2

  D．a+b或a-b
  组卷：1532引用：46难度：0.9

  解析

二、填空题（本大题共12题，每题4分，共48分）

• 7．已知

  a

  b

  =

  2

  3

  ，则

  a

  a

  +

  b

  的值是

  ．
  组卷：1579引用：40难度：0.7

  解析

• 8．线段AB=10cm,点P是AB的黄金分割点，且AP＜BP，则AP=

  ．
  组卷：41引用：3难度：0.7

  解析

三、解答题（本大题共7题，10′×4+12′×2+14′=78分）

• 24．我们定义【a,b,c】为函数y=ax²+bx+c的“特征数”，如：函数y=2x²-3x+5的“特征数”是【2，-3，5】，函数y=x+2的“特征数”是【0，1，2】．
  （1）若一个函数的“特征数”是【1，-4，1】，将此函数图象先向左平移2个单位，再向上平移1个单位，得到一个图象对应的函数“特征数”是

  ；
  （2）将“特征数”是【0，

  -

  3

  3

  ，-1】的图象向上平移2个单位，得到一个新函数，这个函数的解析式是

  ；
  （3）在（2）中，平移前后的两个函数图象分别与y轴交于A、B两点，与直线

  x

  =

  -

  3

  分别交于D、C两点，在给出的平面直角坐标系中画出图形，并求出以A、B、C、D四点为顶点的四边形的面积；
  （4）若（3）中的四边形与“特征数”是【1，-2b,

  b

  2

  +

  1

  2

  】的函数图象有交点，求满足条件的实数b的取值范围．
  组卷：80引用：2难度：0.1

  解析

• 25．在△ABC中，∠BAC=90°，AB＜AC，M是BC边的中点，MN⊥BC交AC于点N．动点P从点B出发沿射线BA以每秒

  3

  厘米的速度运动．同时，动点Q从点N出发沿射线NC运动，且始终保持MQ丄MP．设运动时间为t秒（t＞0）．
  （1）△PBM与△QNM相似吗？以图1为例说明理由；
  （2）若∠ABC=60°，AB=4

  3

  厘米．
  ①求动点Q的运动速度；
  ②设△APQ的面积为S（平方厘米），求S与t的函数关系式．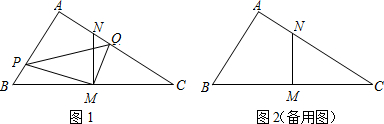
  
  组卷：851引用：5难度：0.5

  解析