2022-2023学年黑龙江省哈尔滨师大附中高一(下)月考数学试卷(4月份)
发布:2024/5/16 8:0:9
一、单选题:本大题共8小题,每个小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.
-
1.sin930°的值是( )
组卷:33引用:3难度:0.9 -
2.已知向量
,则a=(1,2),b=(2,1)=( )|a+b|组卷:122引用:1难度:0.8 -
3.在△ABC中,A=
,BC=6,AB=2π3,则C=( )6组卷:163引用:4难度:0.9 -
4.在△ABC中,若AD为BC边上的中线,点E在AD上,且AE=2ED,则
=( )EB组卷:388引用:15难度:0.8 -
5.为了得到函数y=3cos2x的图象,可以将函数
的图象( )y=3sin(2x+π6)组卷:61引用:1难度:0.7 -
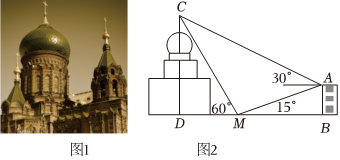 6.小明同学为了估算位于哈尔滨的索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物AB,高为m,在它们之间的地面上的点M(B,M,D三点共线)处测得楼顶A,教堂顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则小明估算索菲亚教堂的高度为( )15(3-1)组卷:316引用:14难度:0.5
6.小明同学为了估算位于哈尔滨的索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物AB,高为m,在它们之间的地面上的点M(B,M,D三点共线)处测得楼顶A,教堂顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则小明估算索菲亚教堂的高度为( )15(3-1)组卷:316引用:14难度:0.5 -
7.已知平面向量
,a满足b,|a|=2,b=(1,1),则|a+b|=10在a上的投影向量的坐标为( )b组卷:559引用:15难度:0.8
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
 21.在近年,中国采用“吹沙填海”的方式,成功将部分小岛礁连成一片,可以进而形成一个大岛礁.已知南海上存在A、F、E、D四个小岛礁,它们在一条直线上且满足AF=FE=ED,若通过“吹沙填海”的方式建成了如图所示一个矩形区域ABCD的大岛礁,其中AD=2AB=120米.
21.在近年,中国采用“吹沙填海”的方式,成功将部分小岛礁连成一片,可以进而形成一个大岛礁.已知南海上存在A、F、E、D四个小岛礁,它们在一条直线上且满足AF=FE=ED,若通过“吹沙填海”的方式建成了如图所示一个矩形区域ABCD的大岛礁,其中AD=2AB=120米.
(1)P为线段BC上一点,求PE2+PF2最小值;
(2)P为线段BC上一点,求cos∠EPF的最小值;
(3)因特殊原因,划定以A圆心,AB为半径的圆的区域为“隔离区”,拟建造一条道路MN,使MN与该“隔离区”的边界相切,求四边形CDNM面积的最大值.14组卷:40引用:3难度:0.5 -
22.已知向量
=(sin2x,cos2x),m=(n,32),函数f(x)=12m.•n
(1)求函数f(x)的解析式和单调递增区间;
(2)若a,b,c分别为△ABC三个内角A,B,C的对边,f(A)=1,b=2,a∈[,12],试判断这个三角形解的个数,并说明理由;52
(3)若x∈[-,π6]时,关于x的方程f(x+2π3)+(λ+1)sinx=λ(λ∈R)恰有三个不同的实根x1,x2,x3,求实数λ的取值范围及x1+x2+x3的值.π6组卷:172引用:5难度:0.4


