2023-2024学年广西贵港市名校高一（上）入学数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．2020年人均可支配收入为2.36万元，2022年达到2.7万元，若2020年至2022年间每年人均可支配收入的增长率都为x,则下面所列方程正确的是（　　）

  A．2.7（1+x）2=2.36	B．2.36（1+x）2=2.7
  C．2.7（1-x）2=2.36	D．2.36（1-x）2=2.7
  组卷：19引用：2难度：0.8

  解析

• 2．在平面直角坐标系中，与直线y=-3x关于x轴对称的直线上有一点（m,6），则m的值为（　　）

  A．3

  B．-2

  C．-3

  D．2
  组卷：76引用：2难度：0.7

  解析

• 3．已知集合A={-1，0，1，2}，B={x|x²-2x≥0}，则A∩B=（　　）

  A．{-1，0}

  B．{2}

  C．{-1，0，2}

  D．{0，1，2}
  组卷：71引用：3难度：0.7

  解析

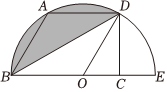• 4．如图，点O是半圆圆心，BE是半圆直径，点A，D在半圆上，且AD∥BO，∠ABO=60°，AB=8，则阴影部分的面积是（　　）

  A． 64 π 3

  B． 32 π 3

  C． 64 π 3 - 8 3

  D． 64 π 3 - 32 3
  组卷：52引用：2难度：0.7

  解析

• 5．“|m|＜1”是“方程x²-mx+1=0无实数解”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：284引用：7难度：0.7

  解析

• 6．已知a＞0，b＞0，a+2b=4，则ab的最大值是（　　）

  A． 2

  B．2

  C． 2 2

  D．4
  组卷：794引用：6难度：0.5

  解析

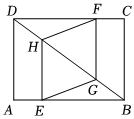• 7．如图，在矩形ABCD中，点E在边AB上，点F在边CD上，点G，H在对角线BD上．若四边形EGFH是菱形，AB=3，BC=2，则AE的长是（　　）

  A． 2 3

  B． 5 6

  C． 5 2

  D． 2 3
  组卷：18引用：2难度：0.6

  解析

四、解答题：本题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤．

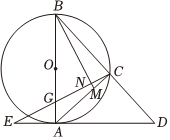• 21．如图，以AB为直径的⊙O是△ABC的外接圆，延长BC到点D，使得∠BAC=∠BDA，点E在DA的延长线上，点M在线段AC上，CE交BM于点N，CE交AB于点G．
  （1）证明：ED是⊙O的切线；
  （2）若DE•AM=AC•AD，证明：BM⊥CE．
  组卷：13引用：2难度：0.7

  解析

• 22．如图，已知抛物线y=ax²-2ax+3与x轴交于点A（-1，0）和点B，与y轴交于点C，连接AC，过B，C两点作直线．
  
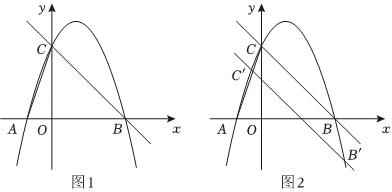
  （1）求a的值．
  （2）将直线BC向下平移m（m＞0）个单位长度，交抛物线于B′，C′两点．在直线B′C′上方的抛物线上是否存在定点D，无论m取何值，都是点D到直线B′C′的距离最大．若存在，请求出点D的坐标；若不存在，请说明理由．
  组卷：9引用：2难度：0.5

  解析