2022-2023学年陕西省西安市长安一中高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分，在每小题所给的四个选项中，只有一项是符合题目要求的.

• 1．复数

  5

  i

  -

  2

  的共轭复数所在的象限是（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：49引用：1难度：0.9

  解析

• 2．为了解学生参加体育锻炼的情况，某学校从高一、高二、高三三个年级中按照分层抽样的方式选取一定数量的学生展开调查．其中高一年级抽取了19人，且高一、高二、高三年级学生人数为760、840、800．则总共抽取的学生人数为（　　）

  A．19

  B．57

  C．60

  D．70
  组卷：61引用：1难度：0.9

  解析

• 3．对于任意两个向量

  a

  ，

  b

  ，下列说法一定正确的是（　　）

  A．若  a ∥ b ，且 | a | ＜ | b | ，则 a ＜ b	B． | a - b | ≤ | a | + | b |
  C． a • b = 0 ，则 | a | = 0 或 | b | = 0	D． | a + b | ≥ | a | + | b |
  组卷：114引用：1难度：0.7

  解析

• 4．在正三棱锥P-ABC中，O是△ABC的中心，PA=AB=2，则

  PO

  •

  （

  PA

  +

  PB

  ）

  等于（　　）

  A． 10 9

  B． 2 6 3

  C． 8 2 3

  D． 16 3
  组卷：350引用：4难度：0.7

  解析

• 5．连掷一枚均匀的骰子两次，所得向上的点数分别为a,b,记m=a+b,则（　　）

  A．事件“m=2”的概率为 1 18

  B．事件“m=2”与“m≠3”对立

  C．事件“m＞11”的概率为 1 18

  D．事件“m是偶数”与“a=b+1”互斥
  组卷：41引用：1难度：0.7

  解析

• 6．底面半径为

  3

  的圆锥侧面展开图的圆心角大小为

  3

  π

  ，则此圆锥外接球表面积为（　　）

  A．16π

  B． 16 π 3

  C． 32 π 3

  D． 32 3 π 27
  组卷：131引用：1难度：0.6

  解析

• 7．在△ABC中，角A，B，C所对的边分别为a,b,c,∠ABC=120°，∠ABC的平分线交AC于点D，且BD=2，则a+2c的最小值为（　　）

  A． 6 + 4 2

  B．12

  C． 3 + 2 2

  D．9
  组卷：188引用：3难度：0.6

  解析

四、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.

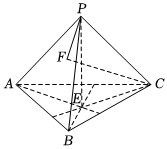• 21．如图所示，在三棱锥P-ABC中，E为P在底面ABC内的投影，且E为△ABC的垂心．
  （1）若F为C在PAB内的投影，证明：PF⊥AB；
  （2）当三棱锥P-ABC为正三棱锥且AB=6，PC与平面ABC所成角为

  π

  4

  时，求点C到平面PAB的距离．
  组卷：50引用：1难度：0.5

  解析

• 22．如图1，在Rt△中，AB⊥BC，AC=12，∠BAC=

  π

  3

  ，E，F都在AC上，且AE：EF：FC=3：4：5，BE∥FG，将△AEB，△CFG分别沿EB，FG折起，使得点A，C在点P处重合，得到四棱锥P-EFGB，如图2．
  （1）求异面直线PF，BG所成角的余弦值；
  （2）若M为PB的中点，求钝二面角B-FM-E的余弦值．
  组卷：64引用：1难度：0.5

  解析