当前位置：试卷中心 > 试卷详情

2022-2023学年辽宁省名校联盟高二（下）月考数学试卷（4月份）

发布：2024/7/5 8:0:9

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知
A
2
n
=
C
2
4
，则n=（　　）
A．5 B．4 C．3 D．2
组卷：42引用：2难度：0.8
解析
2．函数
f
（
x
）
=
1
3
x
在区间[1，8]上的平均变化率为（　　）
A．
-
1
7
B．
-
1
14
C．
1
14
D．
1
7
组卷：97引用：2难度：0.7
解析
3．已知向量
a
=
（
-
2
，
1
，
4
）
，
b
=
（
x
,-
1
2
x
,
3
+
x
）
，若
a
∥
b
，则
|
b
|
=（　　）
A．5 B．
21
C．4 D．
21
2
组卷：342引用：2难度：0.8
解析
4．在等差数列{a_n}中，
1
2
a
14
-
a
10
=
4
，则{a_n}的前11项和为（　　）
A．-88 B．-44 C．44 D．88
组卷：127引用：3难度：0.7
解析
5．1至9中的质数能够组成没有重复数字的整数的个数为（　　）
A．24 B．36 C．48 D．64
组卷：38引用：3难度：0.7
解析
6．足球运动是深受学生喜爱的一项体育运动，为了研究是否喜爱足球运动与学生性别的关系，从某高校男女生中各随机抽取80名学生进行调查问卷，得到如下数据（10≤m≤20，m∈N）：

喜爱不喜爱

男生 70-m 10+m

女生 50+m 30-m

若有90%以上的把握认为是否喜爱足球运动与学生性别有关，则m的最小值为（　　）
附：
χ
2
=
n
（
ad
-
bc
）
2
（
a
+
b
）
（
c
+
d
）
（
a
+
c
）
（
b
+
d
）
．其中n=a+b+c+d.

α=P（χ²≥k） 0.25 0.10 0.05 0.01

k 2.072 2.706 3.841 6.635

A．17 B．15 C．13 D．11
组卷：136引用：2难度：0.8
解析
7．设T_n为数列{a_n}的前n项积，若
a
n
+
2
a
n
+
1
=
0
，
n
∈
N
*
且a₂-a₆=30，则当T_n取得最小值时n=（　　）
A．8 B．7 C．6 D．5
组卷：79引用：2难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

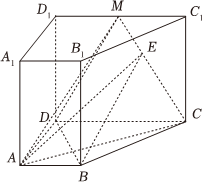21．如图，直四棱柱ABCD-A₁B₁C₁D₁的底面是梯形，∠DAB=∠ADC=90°，CD=3AB=3AD，点M为C₁D₁上一动点，E是MC上一动点．
（1）当CM=4EM随时，证明：AM∥平面BDE；
（2）若△CDM为等边三角形，当直线CM与平面ADE所成的角取得最大值时，求二面角A-DE-B的余弦值．
组卷：37引用：2难度：0.5
解析
22．已知F₁，F₂为椭圆
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左、右焦点，C与抛物线E：y²=-4x有相同的焦点，C与E交于A，B两点，且四边形AF₁BF₂的面积为
4
6
3
．
（1）求C的方程；
（2）设斜率存在的直线l经过M（-1，-2），且l与C交于P，Q两点，线段PQ上是否存在一点H，同时满足下面两个条件，若存在，求出点H的坐标；若不存在，请说明理由．
①|MP|•|HQ|=|MQ|•|HP|；
②|HF₁|+|HF₂|取得最小值．
组卷：36引用：4难度：0.5
解析