2022-2023学年广东省佛山市禅城区荣山中学高二(上)期中数学试卷
发布:2024/9/1 7:0:9
一、单选题(本大题共8小题,每小题5分,共40分)
-
1.若P(A)=0.2,P(B)=0.7且A与B相互独立,则P(AB)=( )
组卷:200引用:3难度:0.9 -
2.若空间中任意四点O,A,B,P满足
=mOP+nOA,其中m+n=1,则( )OB组卷:56引用:4难度:0.7 -
3.若直线过点(2,4),
,则此直线的倾斜角是( )(1,4+3)组卷:700引用:5难度:0.8 -
4.盒子里有4个白球和5个黑球,从中任取一个,取出白球的概率是( )
组卷:8引用:2难度:0.8 -
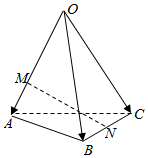 5.如图,空间四边形OABC中,,点M在OA=a,OB=b,OC=c上,且OM=2MA,点N为BC中点,则OA=( )MN组卷:2460引用:155难度:0.9
5.如图,空间四边形OABC中,,点M在OA=a,OB=b,OC=c上,且OM=2MA,点N为BC中点,则OA=( )MN组卷:2460引用:155难度:0.9 -
6.抛掷两枚质地均匀的硬币,设事件A=“第一枚硬币正面朝上”,事件B=“第二枚硬币反面朝上”,则下列说法正确的是( )
组卷:629引用:10难度:0.7 -
7.在空间直角坐标系O-xyz中,已知
,OA=(1,2,3),OB=(2,1,2),点Q在直线OP上运动,则当OP=(1,1,2)取得最小值时,点Q的坐标为( )QA•QB组卷:1027引用:10难度:0.5
四、解答题(本大题共6小题,共70分)
-
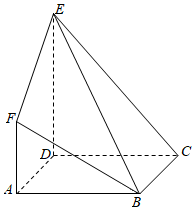 21.如图,在多面体ABCDEF中,梯形ADEF与平行四边形ABCD所在平面互相垂直,AF∥DE,DE⊥AD,AD⊥BE,,AF=AD=12DE=1.AB=2
21.如图,在多面体ABCDEF中,梯形ADEF与平行四边形ABCD所在平面互相垂直,AF∥DE,DE⊥AD,AD⊥BE,,AF=AD=12DE=1.AB=2
(Ⅰ)求证:BF∥平面CDE;
(Ⅱ)求二面角B-EF-D的余弦值;
(Ⅲ)判断线段BE上是否存在点Q,使得平面CDQ⊥平面BEF?若存在,求出的值,若不存在,说明理由.BQBE组卷:709引用:17难度:0.5 -
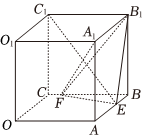 22.如图,在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是棱AB,BC上的动点,且BE=CF.
22.如图,在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是棱AB,BC上的动点,且BE=CF.
(1)求证:A1F⊥C1E;
(2)当三棱锥B1-BEF的体积取得最大值时,求平面EFB1与平面BFB1的夹角的正切值.组卷:13引用:5难度:0.5


