2022-2023学年浙江省丽水市高一（下）期末数学试卷

一、单项选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的

• 1．已知i是虚数单位，复数i（1-2i）=（　　）

  A．1+2i

  B．1-2i

  C．2+i

  D．2-i
  组卷：29引用：2难度：0.9

  解析

• 2．已知向量

  a

  =

  （

  1

  ，

  2

  ）

  ，

  b

  =

  （

  cosθ

  ，

  sinθ

  ）

  ，且向量

  a

  与

  b

  平行，则tanθ的值为（　　）

  A． - 1 2

  B．-2

  C． 1 2

  D．2
  组卷：97引用：2难度：0.8

  解析

• 3．甲、乙两人进行射击比赛，甲的中靶概率为0.4，乙的中靶概率为0.5，则两人各射击一次，恰有一人中靶的概率是（　　）

  A．0.2

  B．0.4

  C．0.5

  D．0.9
  组卷：66引用：2难度：0.7

  解析

• 4．演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分．7个有效评分与9个原始评分相比，不变的数字特征是（　　）

  A．中位数

  B．平均数

  C．方差

  D．极差
  组卷：5886引用：64难度：0.8

  解析

• 5．某中学组织三个年级的学生进行党史知识竞赛．经统计，得到前200名学生分布的扇形图（如图）和前200名中高一学生排名分布的频率条形图（如图），则下列命题错误的是（　　）
  

  A．成绩前200名的学生中，高一人数比高二人数多30人

  B．成绩前100名的学生中，高一人数不超过50人

  C．成绩前50名的学生中，高三人数不超过32人

  D．成绩第51名到第100名的学生中，高二人数比高一人数多
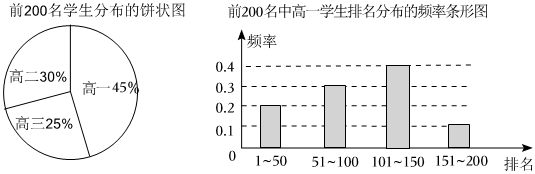  组卷：74引用：7难度：0.7

  解析

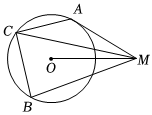• 6．如图，A、B、C三点在半径为1的圆O上运动，且AC⊥BC，M是圆O外一点，OM=2，则

  |

  MA

  +

  MB

  +

  2

  MC

  |

  的最大值是（　　）

  A．5

  B．8

  C．10

  D．12
  组卷：354引用：12难度：0.5

  解析

• 7．一个袋中有大小和质地相同的4个球，其中有2个红球和2个白球，从中一次性随机摸出2个球，则下列说法正确的是（　　）

  A．“恰好摸到1个红球”与“至少摸到1个白球”是互斥事件

  B．“恰好没摸到红球”与“至多摸到1个白球”是对立事件

  C．“至少摸到1个红球”的概率大于“至少摸到1个白球”的概率

  D．“恰好摸到2个红球”与“恰好摸到2个白球”是相互独立事件
  组卷：176引用：3难度：0.7

  解析

四、解答题：本大题共5小题，每小题12分，共60分．解答应写出文字说明、证明过程或演算步骤．

• 22．在△ABC中，三个内角A，B，C所对的边分别是a,b,c,

  AD

  =

  2

  DC

  ，BD=2，且（a-c）sin（A+B）=（a-b）（sinA+sinB）．
  （1）求B；
  （2）当2a+c取最大值时，求△ABC的周长．
  组卷：134引用：2难度：0.5

  解析

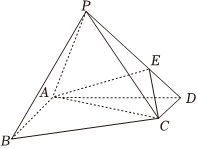• 23．如图，四棱锥P-ABCD中，底面ABCD为直角梯形，AB∥CD，∠BAD=90°，AB=2CD=4，PA⊥CD，在锐角△PAD中，

  AD

  =

  PD

  =

  3

  2

  ，点E在PD上，PE=2ED．
  （1）求证：PB∥平面ACE；
  （2）若AC与平面PCD所成的角为30°，求二面角P-AC-E的正切值．
  组卷：123引用：2难度：0.4

  解析