2020-2021学年浙江省杭州市萧山实验中学八年级（上）月考数学试卷（10月份）

一、选择题（共十题：共30分）

• 1．下列语句是命题的是（　　）

  A．作直线AB的垂线	B．同旁内角互补
  C．在线段AB上取点C	D．垂线段最短吗？
  组卷：308引用：46难度：0.9

  解析

• 2．如果等腰三角形一个底角是30°，那么顶角是（　　）

  A．60°

  B．150°

  C．120°

  D．75°
  组卷：28引用：4难度：0.9

  解析

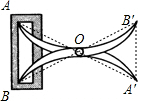• 3．如图，将两根钢条AA'、BB'的中点O连在一起，使AA'、BB'可以绕着点O自由旋转，就做成了一个测量工件，则A'B'的长等于内槽宽AB，那么判定△OAB≌△OA'B'的理由是（　　）

  A．SSS

  B．SAS

  C．AAS

  D．ASA
  组卷：1258引用：24难度：0.5

  解析

• 4．下列四个关于轴对称的判断①对称轴可以是直线、线段或射线；②轴对称图形的对称轴至少有一条；③成轴对称的两个图形全等，全等的两个图形成轴对称；④线段是轴对称图形中，正确的是（　　）

  A．①②

  B．②③

  C．①③

  D．②④
  组卷：11引用：1难度：0.8

  解析

• 5．已知△A₁B₁C₁，△A₂B₂C₂的周长相等，现有两个判断：①若A₁B₁=A₂B₂，A₁C₁=A₂C₂，则△A₁B₁C₁≌△A₂B₂C₂；②若A₁B₁=A₂B₂，∠A₁=∠A₂，则△A₁B₁C₁≌△A₂B₂C₂，对于上述的两个判断，下列说法正确的是（　　）

  A．①正确，②错误	B．①错误，②正确
  C．①②都错误	D．①②都正确
  组卷：27引用：1难度：0.5

  解析

• 6．一个等腰三角形的底边长为5，一腰上中线把其周长分成的两部分的差为3，则这个等腰三角形的腰长为（　　）

  A．2

  B．8

  C．2或8

  D．10
  组卷：190引用：5难度：0.9

  解析

• 7．在等腰三角形中，AB的长是BC的2倍，周长为40，则AB的长为（　　）

  A．16

  B．20

  C．16或20

  D．以上都不对
  组卷：429引用：6难度：0.9

  解析

三、解答题（共七题：共66分）

• 22．已知等腰△ABC中，∠A=80°．
  （1）求∠B的度数．
  （2）在解答完（1）后，小敏发现，∠A的度数不同，得到∠B的度数的个数也可能不同，如果在等腰△ABC中，设∠A=x°，当∠B有三个不同的度数时，请你探索x的取值范围．
  组卷：9引用：1难度：0.5

  解析

• 23．【问题提出】用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
  【问题探究】不妨假设能搭成m种不同的等腰三角形，为探究m与n之间的关系，我们可以先从特殊入手，通过试验、观察、类比、最后归纳、猜测得出结论．
  【探究一】
  （1）用3根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？
  此时，显然能搭成一种等腰三角形．
  所以，当n=3时，m=1．
  （2）用4根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？
  只可分成1根木棒、1根木棒和2根木棒这一种情况，不能搭成三角形．
  所以，当n=4时，m=0．
  （3）用5根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？
  若分成1根木棒、1根木棒和3根木棒，则不能搭成三角形．
  若分成2根木棒、2根木棒和1根木棒，则能搭成一种等腰三角形．
  所以，当n=5时，m=1．
  （4）用6根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？
  若分成1根木棒、1根木棒和4根木棒，则不能搭成三角形．
  若分成2根木棒、2根木棒和2根木棒，则能搭成一种等腰三角形．
  所以，当n=6时，m=1．
  综上所述，可得：表①
  

  n	3	4	5	6
  m	1	0	1	1

  【探究二】
  （1）用7根相同的木棒搭一个三角形，能搭成多少种不同的三角形？
  （仿照上述探究方法，写出解答过程，并将结果填在表②中）
  （2）用8根、9根、10根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？
  （只需把结果填在表②中）
  表②
  

  n	7	8	9	10
  m

  你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究，…
  【问题解决】：用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（设n分别等于4k-1，4k,4k+1，4k+2，其中k是正整数，把结果填在表③中）
  表③
  

  n	4k-1	4k	4k+1	4k+2
  m

  【问题应用】：用2016根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（写出解答过程），其中面积最大的等腰三角形每腰用了

   

  根木棒．（只填结果）
  组卷：776引用：28难度：0.3

  解析