2022-2023学年山东省淄博市周村区七年级(下)期中数学试卷(五四学制)
发布:2024/7/9 8:0:8
一、选择题。(在每小题给出的四个选项中,只有一个是正确的,请把正确的选项填在题后的括号内,每小题5分,共60分)
-
1.下列命题中为假命题的是( )
组卷:134引用:4难度:0.7 -
2.如果
是关于x,y的方程mx+2y=6的解,那么m的值为( )x=1y=2组卷:195引用:5难度:0.7 -
3.把一副普通扑克牌中的5张洗匀后,正面向下放在桌子上,其中有1张“黑桃”,2张“梅花”和2张“红桃”,从中随机抽取一张,恰好是“梅花”的概率是( )
组卷:79引用:3难度:0.6 -
4.一只不透明的袋子中装有3个黑球和2个白球,这些除颜色外无其他差别,从中任意摸出3个球,下列事件是必然事件的为( )
组卷:487引用:14难度:0.9 -
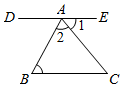 5.如图,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( )组卷:785引用:9难度:0.6
5.如图,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( )组卷:785引用:9难度:0.6 -
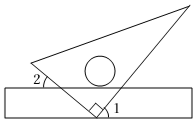 6.将含30°的直角三角板与直尺如图所示放置,若∠2=40°,则∠1的度数为( )组卷:597引用:14难度:0.6
6.将含30°的直角三角板与直尺如图所示放置,若∠2=40°,则∠1的度数为( )组卷:597引用:14难度:0.6 -
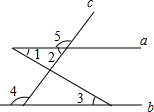 7.如图,下列条件中,不能判断直线a∥b的是( )组卷:7523引用:91难度:0.9
7.如图,下列条件中,不能判断直线a∥b的是( )组卷:7523引用:91难度:0.9 -
8.一次函数y=2x+b经过点(0,-4),那么b的值为( )
组卷:255引用:5难度:0.6
三、解答题。解答要写出必要的文字说明或演算步骤.(共70分)
-
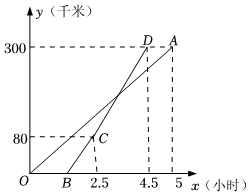 23.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发开往乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
23.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发开往乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
(1)求线段CD对应的函数解析式.
(2)货车从甲地出发后多长时间被轿车追上?此时离甲地的距离是多少千米?
(3)轿车到达乙地后,货车距乙地多少千米.组卷:278引用:4难度:0.1 -
24.阅读下列材料:
如图1,AB∥CD,E,F分别是AB,CD上的点,点P在AB,CD之间,连接PE,PF.我们可以通过作辅助线证明结论:∠EPF=∠AEP+∠CFP.
请你利用这个结论或证明思路,完成下列问题.
已知AB∥CD,E,F分别是AB,CD上的点,点P在AB,CD之间,连接PE,PF.
(1)如图2,若∠AEP=45°,∠EPF=80°,请直接写出∠PFD的度数;
(2)如图3,∠AEP与∠CFP的平分线交于点Q,用等式表示∠EPF与∠EQF的数量关系,并证明;
(3)如图4,∠AEP与∠CFP的平分线交于点Q,直接用等式表示∠EPF与∠EQF的数量关系.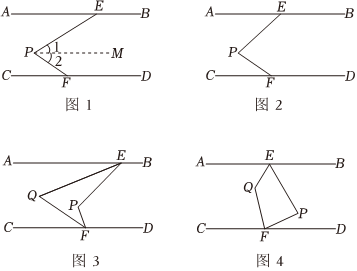 组卷:149引用:1难度:0.6
组卷:149引用:1难度:0.6


