当前位置：试卷中心 > 试卷详情

2022-2023学年福建省泉州市石狮实验中学九年级（上）期中数学试卷

发布：2024/9/25 17:0:4

一、选择题（共10小题，满分40分，每小题4分）

1．若二次根式
x
-
3
有意义，则x的值可以为（　　）
A．-2 B．4 C．2 D．0
组卷：532引用：9难度：0.9
解析
2．下列根式是最简二次根式的是（　　）
A．
8
B．
27
C．
3
3
D．
1
2
组卷：459引用：6难度：0.7
解析
3．已知
a
b
=
3
5
，则代数式
a
+
b
b
的值为（　　）
A．
8
5
B．
5
3
C．
3
5
D．
8
3
组卷：203引用：4难度：0.9
解析
4．解一元二次方程x²-6x+2=0，用配方法可变形为（　　）
A．（x-3）²=9 B．（x+3）²=9 C．（x-3）²=11 D．（x-3）²=7
组卷：478引用：11难度：0.7
解析
5．下列各组中的四条线段成比例的是（　　）
A．4cm,3cm,2cm,1cm B．6cm,2cm,3cm,5cm
C．4cm,8cm,10cm,5cm D．8cm,6cm,7cm,5cm
组卷：21引用：2难度：0.6
解析
6．某农机厂四月份生产零件50万个，第二季度共生产零件182万个．设该厂第二季度平均每月的增长率为x,那么x满足的方程是（　　）
A．50（1+x）²=182
B．50+50（1+x）+50（1+x）²=182
C．50（1+x）+50（1+x）²=182
D．50+50（1+x）=182
组卷：996引用：18难度：0.8
解析
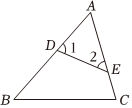7．如图，△ABC中，点D、E分别在AB、AC边上，则下列条件中，不一定能使△AED∽△ABC的是（　　）
A．∠2=∠B B．∠1=∠C C．
AE
AB
=
AD
AC
D．
AD
AB
=
DE
BC
组卷：1855引用：21难度：0.9
解析
8．下列判断正确的是（　　）
A．所有的等腰三角形都相似
B．所有的直角三角形都相似
C．所有的正方形都相似
D．所有的菱形都相似
组卷：34引用：2难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共9小题，满分86分）

24．阅读材料：
材料1：一元二次方程ax²+bx+c=0（a≠0，b²-4ac≥0）的两根x₁，x₂有如下的关系（韦达定理）：x₁+x₂=-
b
a
，x₁•x₂=
c
a
．
材料2：有些数学问题虽然表面与一元二次方程无关，但是我们能够通过构造一元二次方程，并利用一元二次方程的有关知识将其解决．下面介绍两种基本构造方法：
方法1：利用根的定义构造．例如，如果实数m、n满足m²-m-1=0、n²-n-1=0，且m≠n,则可将m、n看作是方程x²-x-1=0的两个不相等的实数根．
方法2：利用韦达定理逆向构造．例如，如果实数a、b满足a+b=3、ab=2，则可以将a、b看作是方程x²-3x+2=0的两实数根．
根据上述材料解决下面问题：
（1）已知实数m、n满足3m²-m-2=0，3n²-n-2=0，求
n
m
+
m
n
的值．
（2）已知实数a、b、c满足a+b=c-5，ab=
16
5
-
c
，且c＜5，求c的最大值．
组卷：478引用：5难度：0.6
解析
25．如图1，在平面直角坐标系中，直线
y
=
1
2
x
+
2
分别与x轴、y轴交于A、C两点，过点作BC⊥AC，交x轴于点B．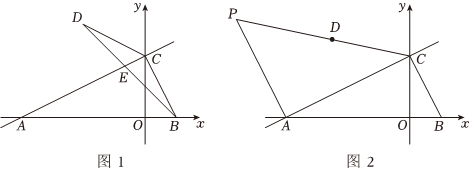

（1）直接写出点A的坐标；
（2）若点
D
（
t
,-
1
2
t
2
-
3
2
t
+
2
）
在第二象限，且在直线AC上方．
①连接CD，BD，设线段AC、BD交于点E，求
DE
BE
的最大值；
②如图2，过点A作AP⊥AC，交CD延长线于点P，若∠APC=2∠BAC，求t的值．
组卷：13引用：3难度：0.5
解析