2023-2024学年江苏省盐城市东台市第五联盟八年级（上）月考数学试卷（10月份）

一、选择题（本大题共8小题，每小题3分，共24分）

• 1．如图所示的图形是全等图形的是（　　）

  A．	B．
  C．	D．
  组卷：1819引用：10难度：0.7

  解析

• 2．如图，已知AB=AD，添加下列一个条件后，仍无法判定△ABC≌△ADC的是（　　）

  A．CB=CD

  B．∠BCA=∠DCA

  C．∠BAC=∠DAC

  D．∠B=∠D=90°
  组卷：495引用：13难度：0.7

  解析

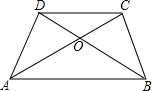• 3．如图，AC、BD相交于点O，OA=OB，OC=OD，则图中全等三角形的对数是（　　）

  A．1对

  B．2对

  C．3对

  D．4对
  组卷：752引用：7难度：0.6

  解析

• 4．如图，在△ABC中，AC=BC，∠A=40°，观察图中尺规作图的痕迹，可知∠ACG的度数为（　　）

  A．40°

  B．45°

  C．50°

  D．60°
  组卷：238引用：3难度：0.5

  解析

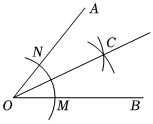• 5．用直尺和圆规作一个角的平分线的示意图如图所示，则能说明∠AOC=∠BOC的依据是（　　）

  A．（AAS）

  B．（SAS）

  C．（ASA）

  D．（SSS）
  组卷：589引用：34难度：0.7

  解析

• 6．下列四组三角形中，一定是全等三角形的是（　　）

  A．三个内角分别对应相等的两个三角形

  B．两条边和第三边上的中线对应相等的两个三角形

  C．两条边和其中一个角对应相等的两个三角形

  D．两条边和第三边上的高对应相等的两个三角形
  组卷：144引用：2难度：0.5

  解析

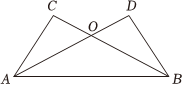• 7．如图，∠CAB=∠DBA，AC=BD，则下列结论中，不正确的是（　　）

  A．BC=AD

  B．CO=DO

  C．∠C=∠D

  D．∠AOB=∠C+∠D
  组卷：143引用：4难度：0.9

  解析

• 8．如图是4×4正方形网格，其中已有3个小正方形涂成了黑色，现在要从其余13个白色小方格中选出一个也涂成黑色的图形称为轴对称图形，这样的白色小方格有（　　）

  A．2个

  B．3个

  C．4个

  D．5个
  组卷：1309引用：18难度：0.7

  解析

三.解答题（本大题共9小题，共72分）.

• 24．如图，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，点E、F分别在直线BC、CD上，且∠EAF=

  1

  2

  ∠BAD．
  （1）当点E、F分别在边BC、CD上时（如图1），请说明EF=BE+FD的理由；
  （2）当点E、F分别在边BC、CD延长线上时（如图2），（1）中的结论是否仍然成立？若成立，请说明理由；若不成立，请写出EF、BE、FD之间的数量关系，并说明理由．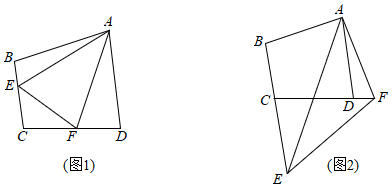
  
  组卷：831引用：2难度：0.4

  解析

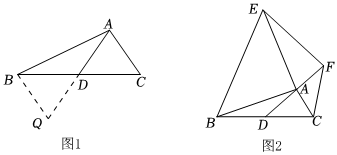• 25．阅读理解：课外兴趣小组活动时，老师提出了如下问题：在△ABC中，AB=7，AC=3，求BC边上的中线AD的取值范围．
  （1）小明在组内经过合作交流，得到了如下的解决方法（如图1）：
  ①延长AD到Q使得DQ=AD；
  ②再连接BQ，把AB、AC、2AD集中在△ABQ中；③利用三角形的三边关系可得4＜AQ＜10，则AD的取值范围是

  ．
  感悟：解题时，条件中若出现“中点”“中线”等条件，可以考虑倍长中线，构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中．
  （2）请写出图1中AC与BQ的位置关系并证明；
  （3）思考：已知，如图2，AD是△ABC的中线，AB=AE，AC=AF，∠BAE=∠FAC=90°，试探究线段AD与EF的数量和位置关系，并加以证明．
  组卷：896引用：17难度：0.4

  解析