当前位置：试卷中心 > 试卷详情

2022-2023学年广东省广州七十五中高三（上）月考数学试卷（10月份）

发布：2024/8/18 17:0:1

一、单选题（共40分，每小题5分）

1．已知集合
A
=
{
y
|
y
=
x
+
1
}
，集合B={x|x＜1}，则A∩B=（　　）
A．[-1，1） B．（-1，1） C．（-∞，1） D．[0，1）
组卷：20引用：3难度：0.8
解析
2．已知角x的终边上一点坐标为
（
sin
5
π
6
，
cos
5
π
6
）
，则角x的最小正值为（　　）
A．
5
π
6
B．
5
π
3
C．
11
π
6
D．
2
π
3
组卷：126引用：12难度：0.9
解析
3．若sin（
α
+
π
4
）=
1
3
，则sin2α=（　　）
A．-
7
9
B．
7
9
C．
1
-
2
3
D．
2
2
3
组卷：238引用：5难度：0.6
解析
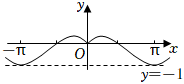4．函数f（x）的部分图象如图所示，则f（x）的解析式可能为（　　）
A．f（x）=
3
xsinx
1
+
2
x
2
B．f（x）=
x
2
sinx
1
+
x
2
C．f（x）=
3
x
2
cosx
1
+
2
x
2
D．f（x）=
x
2
cosx
1
+
x
2
组卷：253引用：7难度：0.8
解析
5．定义“等方差数列”：如果一个数列从第二项起，每一项的平方与它的前一项的平方的差都等于同一个常数，那么这个数列就叫作等方差数列，这个常数叫作该数列的方公差．设{a_n}是由正数组成的等方差数列，且方公差为
2
，
a
9
=
3
2
，则数列
{
2
a
n
+
a
n
+
1
}
的前24项和为（　　）
A．
4
2
B．4 C．
3
2
D．6
组卷：96引用：3难度：0.6
解析
6．将5个1和2个0随机排成一行，则2个0不相邻的概率为（　　）
A．
3
7
B．
5
7
C．
2
5
D．
3
5
组卷：77引用：4难度：0.7
解析
7．已知A，B是圆C₁：x²+y²=1上的动点，AB=
3
，P是圆C₂：（x-3）²+（y-4）²=1上的动点，则|
PA
+
PB
|的取值范围为（　　）
A．[
7
2
，
13
2
] B．[3，6] C．[7，13] D．[6，12]
组卷：241引用：8难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（共70分）

21．2022年是中国共产主义青年团成立100周年，某市团委决定举办一次共青团史知识擂台赛．该市A县团委为此举办了一场选拔赛，选拔赛分为初赛和决赛，初赛通过后才能参加决赛，决赛通过后将代表A县参加市赛．已知A县甲、乙、丙3位选手都参加初赛且通过初赛的概率均为
4
5
，通过初赛后再通过决赛的概率依次为
5
8
，
5
12
，
5
16
假设他们之间通过与否互不影响．
（1）求这3人中至少有1人通过初赛的概率；
（2）设这3人中参加市赛的人数为ξ，求ξ的分布列；
（3）某品牌商赞助了A县的这次共青团史知识擂台赛，提供了两种奖励方案：
方案1：参加了选拔赛的选手都可参与抽奖，每人抽奖1次，每次中奖的概率均为
2
3
，且每次抽奖互不影响，中奖一次奖1000元；
方案2：参加了选拔赛未进市赛的选手一律奖600元，进入了市赛的选手奖1200元．
若品牌商希望给予选手更多的奖励，试从三人奖金总额的数学期望的角度分析，品牌商选择哪种方案更好．
组卷：274引用：6难度：0.5
解析
22．已知点
P
（
1
，
3
2
）
在椭圆C：
x
2
a
2
+
y
2
b
2
=
1
（a＞b＞0）上，且点P到椭圆右顶点M的距离为
13
2
．
（1）求椭圆C的方程；
（2）若点A，B是椭圆C上不同的两点（均异于M）且满足直线MA与MB斜率之积为
1
4
．试判断直线AB是否过定点，若是，求出定点坐标，若不是，说明理由．
组卷：32引用：2难度：0.6
解析