2023-2024学年湖南省衡阳八中高三（上）段考数学试卷（二）

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知复数z是一元二次方程x²-2x+2=0的一个根，则|z|的值为（　　）

  A．1

  B． 2

  C．0

  D．2
  组卷：487引用：11难度：0.9

  解析

• 2．已知集合A={x|x²-8x＜0}，B={x|x=3k-1，k∈N}，则A∩B=（　　）

  A．{-1，2，5，8}

  B．{-1，2，5}

  C．{2，5，8}

  D．{2，5}
  组卷：78引用：3难度：0.8

  解析

• 3．已知m＞0，则“a＞b＞0”是“

  b

  +

  m

  a

  +

  m

  ＞

  b

  a

  ”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：108引用：4难度：0.7

  解析

• 4．已知（

  x

  +

  a

  x

  ）⁸的展开式中各项系数之和为0，则展开式中x的系数为（　　）

  A．28

  B．-28

  C．45

  D．-45
  组卷：327引用：3难度：0.7

  解析

• 5．已知x＞0，y＞0，且（

  1

  2

  ）^x=x,2^y=log_yx,则（　　）

  A．0＜y＜x＜1

  B．0＜x＜y＜1

  C．x＞y＞1

  D．y＞x＞1
  组卷：97引用：3难度：0.7

  解析

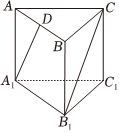• 6．直三棱柱ABC-A₁B₁C₁如图所示，AB=4，BC=3，AC=5，D为棱AB的中点，三棱柱的各顶点在同一球面上，且球的表面积为61π，则异面直线A₁D和B₁C所成的角的余弦值为（　　）

  A． 3 2 5

  B． 2 5

  C． 4 2 5

  D． 16 2 25
  组卷：351引用：7难度：0.6

  解析

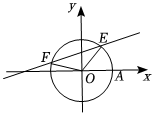• 7．如图，在平面直角坐标系中，以OA为始边，角α与β的终边分别与单位圆相交于E，F两点，且

  α

  ∈

  （

  0

  ，

  π

  2

  ）

  ，

  β

  ∈

  （

  π

  2

  ，

  π

  ）

  ，若直线EF的斜率为

  1

  4

  ，则sin（α+β）=（　　）

  A． - 15 17

  B． - 8 17

  C． 8 17

  D． 15 17
  组卷：198引用：4难度：0.6

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知函数f（x）=xlnx-ax²+3x.
  （1）若对任意的x∈（0，+∞），f（x）≤1恒成立，求实数a的取值范围；
  （2）证明：当n∈N^*时，

  3

  1

  ×

  2

  +

  4

  2

  ×

  3

  +

  5

  3

  ×

  4

  +

  …

  +

  n

  +

  2

  n

  （

  n

  +

  1

  ）

  ≥

  ln

  （

  n

  +

  1

  ）

  ．
  组卷：158引用：4难度：0.5

  解析

• 22．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）的离心率为

  2

  2

  ，三点

  M

  1

  （

  -

  2

  ，

  2

  ）

  ，

  M

  2

  （

  2

  ，-

  2

  ）

  ，

  M

  3

  （

  2

  ，

  3

  2

  ）

  中恰有两个点在椭圆上．
  （Ⅰ）求椭圆C的方程；
  （Ⅱ）若C的上顶点为E，右焦点为F，过点F的直线交C于A，B两点（与椭圆顶点不重合），直线EA，EB分别交直线x-y-4=0于P，Q两点，求△EPQ面积的最小值．
  组卷：502引用：6难度：0.4

  解析