2022-2023学年河南省平顶山市七年级（下）期末数学试卷

一、选择题（每小题3分，共30分，下列各小题均有四个选项，其中只有一个是正确的．）

• 1．下列各数中，小于0的数是（　　）

  A．（-1）0

  B．|-1|

  C． 1

  D．-12
  组卷：59引用：3难度：0.9

  解析

• 2．从“同一个世界，同一个梦想”的2008年夏季奥运会，到“一起向未来”的2022年冬季奥运会，北京成为世界上首座“双奥之城”，下列四幅图是两届奥运会的参选徽标，其中文字上方的图案是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：72引用：2难度：0.9

  解析

• 3．下列事件中的必然事件是（　　）

  A．任意买一张电影票，座位号是2的倍数

  B．打开电视机，它正在播放“朗读者”

  C．将油滴入水中，油会浮在水面上

  D．早上的太阳从西方升起
  组卷：264引用：3难度：0.9

  解析

• 4．皮米是较小的长度单位，已知1皮米=0.001纳米，1纳米=10^-9米，则1皮米等于（　　）

  A．10-13米

  B．10-12米

  C．10-11米

  D．10-10米
  组卷：36引用：1难度：0.7

  解析

• 5．已知某三角形的两边长分别为2和4，且第三边为偶数，则该三角形周长为（　　）

  A．10

  B．11

  C．12

  D．13
  组卷：106引用：1难度：0.6

  解析

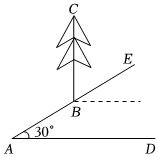• 6．如图，一棵树生长在30°的山坡AE上，树干BC垂直于水平线AD，则∠ABC的度数为（　　）
  

  A．120°

  B．125°

  C．130°

  D．135°
  组卷：53引用：2难度：0.7

  解析

• 7．如图，AD是△ABC的中线，以点D为圆心，AD的长为半径画弧，交AD的延长线于点E．连接BE，下列结论不一定成立的是（　　）

  A．△ADC≌△EDB

  B．AD=BD

  C．∠C=∠DBE

  D．AC∥BE
  组卷：177引用：2难度：0.5

  解析

三、解答题：（本大题共8个小逐，满分75分）

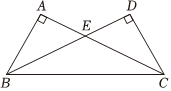• 22．如图，∠BAC=∠CDB=90°，AB=DC，AC与BD相交于点E．
  （1）图中有对全等的三角形，请你选择一对全等三角形，并说明理由；
  （2）连接AD，判断AD与BC的位置关系，并说明理由．
  组卷：104引用：1难度：0.5

  解析

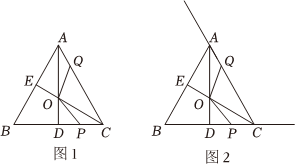• 23．如图1，△ABC是等边三角形，AD，CE是△ABC的角平分线，AD与CE相交于点O．点P在线段DC上，点Q在边AC上，且BP=CQ．连接OP，OQ．
  （1）聪聪研究发现OA=OC．
  理由如下：因为AD是△ABC的角平分线，且

  .

  A

  B

  =

  AC

  ，根据等腰三角形的性质①，可得AD⊥BC，且BD=DC，即AD垂直平分BC，同理，CE垂直平分AB，所以点O是△ABC三边中垂线的交点，根据线段垂直平分线的性质②，可得OA=OC．
  填空：上述证明过程中，①、②两处的理由分别为

  和

  ；（填选项前的字母）
  a.“三线合一”；b.线段垂直平分线上的点到这条线段两个端点的距离相等；c.等腰三角形两个底角相等．
  （2）判断OQ和OP的数量关系，并说明理由；
  （3）如图2，若点P是射线DC上任意一点，点Q在射线CA上，其它条件不变，当△OPC为等腰三角形时，直接写出∠COQ的度数．
  组卷：256引用：4难度：0.5

  解析