当前位置：试卷中心 > 试卷详情

2021-2022学年江苏省连云港市连云区东港中学九年级（上）第二次质检数学试卷（12月份）

发布：2024/7/26 8:0:9

一、选择题（每题3分，共24分）

1．抛物线y=2（x+3）²-5的顶点坐标是（　　）
A．（-3，-5） B．（-3，5） C．（3，-5） D．（3，5）
组卷：879引用：17难度：0.9
解析
2．一组数据4，4，5，5，x,6，7的平均数是5，则这组数据的众数和中位数分别是（　　）
A．4，5 B．4，4 C．5，4 D．5，5
组卷：747引用：8难度：0.7
解析
3．若A（-4，y₁），B（-3，y₂），C（1，y₃）为二次函数y=x²+4x-5的图象上的三点，则y₁，y₂，y₃的大小关系是（　　）
A．y₁＜y₂＜y₃ B．y₂＜y₁＜y₃ C．y₃＜y₁＜y₂ D．y₁＜y₃＜y₂
组卷：1401引用：53难度：0.9
解析
4．如图，沿一条母线将圆锥侧面剪开并展开，得到一个扇形，若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°，则该圆锥的母线长为（　　）
A．6cm B．7cm C．8cm D．9cm
组卷：252引用：6难度：0.7
解析
5．已知：如图，OA，OB是⊙O的两条半径，且OA⊥OB，点C在⊙O上，则∠ACB的度数为（　　）
A．45° B．35° C．25° D．20°
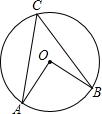组卷：631引用：95难度：0.9
解析
6．若3a=2b,则
a
b
的值为（　　）
A．
2
3
B．
3
2
C．
3
5
D．
5
3
组卷：173引用：2难度：0.9
解析
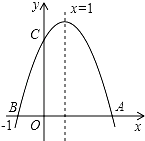7．如图，若二次函数y=ax²+bx+c（a≠0）图象的对称轴为直线x=1，与y轴交于点C，与x轴交于点A、点B（-1，0），则：①二次函数的最大值为a+b+c；②a-b+c＜0；③b²-4ac＞0；④当时y＞0，-1＜x＜3；其中正确的个数是（　　）
A．1个 B．2个 C．3个 D．4个
组卷：338引用：2难度：0.8
解析
8．已知二次函数y=（x-h）²+1（h为常数），在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最小值为10，则h的值为（　　）
A．-2或4 B．0或6 C．1或3 D．-2或6
组卷：2633引用：7难度：0.8
解析

二．填空题（共10小题，共30分）

9．相距24千米的甲、乙两地，在比例尺为1：400000的地图上的距离是
厘米．
组卷：93引用：2难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三．解答题（共9小题，共96分）

26．已知，如图，抛物线y=-
1
2
（x-2）²+8与x轴分别交于B，C两点（点C在点B的左边），与y轴交于点A，点P是线段AB上方抛物线上的一个动点．
（1）求A、B、C三点坐标；
（2）求直线AB的解析式；
（3）过点P作x轴的垂线，交线段AB于点D，再过点P作PE∥x轴交抛物线于点E，连结DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标，若不存在，请说明理由．
组卷：398引用：2难度：0.5
解析
27．【问题情境】（1）点A是⊙O外一点，点P是⊙O上一动点．若⊙O的半径为2，且OA=5，则点P到点A的最短距离为
．
【直接运用】（2）如图1，在Rt△ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于D，P是弧CD上的一个动点，连接AP，则AP的最小值是
．
【构造运用】（3）如图2，已知正方形ABCD的边长为6，点M、N分别从点B、C同时出发，以相同的速度沿边BC、CD方向向终点C和D运动，连接AM和BN交于点P，则点P到点C的最短距离，并说明理由．
【灵活运用】（4）如图3，⊙O的半径为4，弦AB=4，点C为优弧AB上一动点，AM⊥AC交直线CB于点M，则△ABM的面积最大值是
．
组卷：1521引用：2难度：0.2
解析