当前位置：试卷中心 > 试卷详情

2022-2023学年北京四十三中九年级（上）期中数学试卷

发布：2024/9/11 4:0:9

一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有一个.

1．围棋起源于中国，古代称之为“弈”，至今已有4000多年的历史．以下是在棋谱中截取的四个部分，由黑白棋子摆成的图案是中心对称图形的是（　　）
A． B． C． D．
组卷：789引用：27难度：0.9
解析
2．抛物线y=（x+1）²+2的顶点坐标为（　　）
A．（-1，2） B．（1，2） C．（1，-2） D．（2，1）
组卷：140引用：6难度：0.7
解析
3．将抛物线y=-2x²向上平移3个单位长度，再向右平移2个单位长度，所得到的抛物线为（　　）
A．y=-2（x+2）²+3 B．y=-2（x-2）²+3
C．y=-2（x-2）²-3 D．y=-2（x+2）²-3
组卷：259引用：8难度：0.7
解析
4．关于x的一元二次方程x²-4x+m=0有两个不相等的实数根，则m的值可能是（　　）
A．3 B．4 C．5 D．6
组卷：212引用：6难度：0.7
解析
5．如图，在平面直角坐标系中，△ABC绕某点旋转90°得到△A'B'C'，则旋转中心是点（　　）
A．O B．M C．N D．无法确定
组卷：506引用：7难度：0.6
解析
6．科学兴趣小组的同学们，将自己收集的标本向本组的其他成员各赠送一件，全组共互赠了132件，设全组共有x名学生，则x满足的方程是（　　）
A．
1
2
x
（
x
+
1
）
=
132
B．x（x+1）=132
C．
1
2
x
（
x
-
1
）
=
132
D．x（x-1）=132
组卷：182引用：11难度：0.7
解析
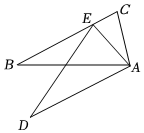7．如图，△ABC中，∠B=35°，∠BAC=70°，将△ABC绕点A旋转逆时针旋转α度（0＜α＜180）后得到△ADE，点E恰好落在BC上，则α=（　　）
A．30° B．35° C．40° D．不能确定
组卷：1339引用：16难度：0.7
解析
8．如图为某二次函数的部分图象，有如下四个结论：
①此二次函数表达式为y=
1
4
x²-x+9；
②若点B（-1，n）在这个二次函数图象上，则n＞m；
③该二次函数图象与x轴的另一个交点为（-4，0）；
④当0＜x＜6时，m＜y＜8．
所有正确结论的序号是（　　）
A．①③ B．①④ C．②③ D．②④
组卷：576引用：8难度：0.6
解析

二、填空题（本题共16分，每小题2分）

9．在平面直角坐标系中，点P（-1，-3）关于原点的对称点坐标为
．
组卷：106引用：10难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题共68分，第17-22题每题5分，第23-26题每题6分，第27、28题每题7分）x2-6x+4=0

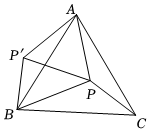27．如图，在等边三角形ABC中，点P为△ABC内一点，连接AP，BP，CP，将线段AP绕点A顺时针旋转60°得到AP'，连接PP'，BP'．
（1）用等式表示BP'与CP的数量关系，并证明；
（2）当∠BPC=120°时，
①直接写出∠P'BP的度数为
；
②若M为BC的中点，连接PM，用等式表示PM与AP的数量关系，并证明．
组卷：2050引用：23难度：0.3
解析
28．定义：在平面直角坐标系中，图形G上点P（x,y）的纵坐标y与其横坐标x的差y-x称为P点的“坐标差”，而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”．
（1）①点A（1，3）的“坐标差”为
；
②抛物线y=-x²+3x+3的“特征值”为
；
（2）某二次函数y=-x²+bx+c（c≠0）的“特征值”为1，点B（m,0）与点C分别是此二次函数的图象与x轴和y轴的交点，且点B与点C的“坐标差”相等．
①直接写出m=
；（用含c的式子表示）
②求b的值．
组卷：606引用：4难度：0.4
解析