当前位置：试卷中心 > 试卷详情

2022-2023学年湖南省永州市冷水滩区京华中学八年级（上）月考数学试卷（12月份）

发布：2024/8/24 0:0:8

一、选择题（每小题4分，共40分）

1．下列各式中，是分式的是（　　）
A．
2
3
B．
a
+
3
b
2
C．
2
xy
π
D．
3
n
+
2
m
组卷：67引用：3难度：0.8
解析
2．不改变分式
0
.
5
x
-
1
0
.
3
x
+
2
的值，把它的分子和分母中的各项系数都化为整数，则所得结果为（　　）
A．
5
x
-
1
3
x
+
2
B．
5
x
-
10
3
x
+
20
C．
2
x
-
1
3
x
+
2
D．
x
-
2
3
x
+
20
组卷：1219引用：41难度：0.9
解析
3．以下各组数为边长，不能组成三角形的是（　　）
A．10，11，20 B．4，5，6 C．7，7，2 D．3，6，3
组卷：4引用：1难度：0.7
解析
4．下列式子：①（-2）^-2=
1
4
；②a⁰=1；③3a^-2=
1
3
a
2
；④-7.02×10^-4=-0.000702．其中正确的式子有（　　）
A．1个 B．2个 C．3个 D．4个
组卷：157引用：3难度：0.7
解析
5．若关于x的分式方程
x
x
-
2
=2-
m
2
-
x
的解为正数，则满足条件的正整数m的值为（　　）
A．1，2，3 B．1，2 C．1，3 D．2，3
组卷：2037引用：14难度：0.7
解析
6．和三角形三个顶点的距离相等的点是（　　）
A．三条角平分线的交点
B．三边中线的交点
C．三边上高所在直线的交点
D．三边的垂直平分线的交点
组卷：4551引用：117难度：0.9
解析
7．不等式组
3
x
-
1
＞
2
8
-
4
x
≤
0
的解集在数轴上表示为（　　）
A． B． C． D．
组卷：6754引用：102难度：0.9
解析
8．将一副三角板按如图所示摆放，图中∠α的度数是（　　）
A．75° B．90° C．120° D．105°
组卷：219引用：9难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（第19题10分，20题6分，21题8分，22、23、24题各10分，25、26题各12分）

25．（1）如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m,CE⊥直线m,垂足分别为点D、E．证明：DE=BD+CE．
（2）如图2，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．
（3）拓展与应用：如图3，D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．
组卷：11340引用：145难度：0.5
解析
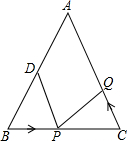26．如图，已知△ABC中，AB=AC=16厘米，BC=10厘米，点D为AB的中点．
（1）如果点P在线段BC上以2厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？
组卷：448引用：7难度：0.5
解析