2023-2024学年江西省抚州市乐安二中高二（上）入学数学试卷

一、单选题（每题5分，共40分）

• 1．已知集合M={x|x（x-2）＜0}，N={-2，-1，0，1，2}，则M∩N=（　　）

  A．{0，1，2}

  B．{-2，-1}

  C．{1}

  D．{-2，-1，0，2}
  组卷：341引用：6难度：0.9

  解析

• 2．已知复数z的共轭复数是

  z

  ，若2

  z

  -z=1-i,则|z|=（　　）

  A．1

  B． 10 3

  C． 2

  D． 30 3
  组卷：231引用：4难度：0.9

  解析

• 3．已知空间中的两个不同的平面α，β，直线m⊥平面β，则“α⊥β”是“m∥α”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充分必要条件	D．既不充分又不必要条件
  组卷：124引用：12难度：0.7

  解析

• 4．若

  tan

  （

  π

  4

  -

  α

  ）

  =

  -

  2

  ，则

  sinα

  sin

  2

  αcosα

  +

  3

  cos

  3

  α

  =（　　）

  A． 5 2

  B．2

  C． - 5 2

  D． - 1 2
  组卷：159引用：4难度：0.8

  解析

• 5．在△ABC中，

  cos

  c

  2

  =

  5

  5

  ，BC=2，AC=5，则AB=（　　）

  A． 2 3

  B． 7

  C． 29

  D． 41
  组卷：130引用：4难度：0.7

  解析

• 6．设

  a

  =

  tan

  23

  °

  1

  -

  tan

  2

  23

  °

  ，b=2sin13°cos13°，c=

  1

  -

  cos

  50

  °

  2

  ，则有（　　）

  A．c＜b＜a

  B．a＜b＜c

  C．a＜c＜b

  D．b＜c＜a
  组卷：237引用：6难度：0.6

  解析

• 7．在平面四边形ABCD中，AB=BC=2CD=2，∠ABC=60°，∠ADC=90°，若P为边BC上的一个动点，则

  PA

  •

  PC

  的最小值是（　　）

  A．-1

  B．- 1 4

  C．- 1 2

  D． 1 4
  组卷：101引用：6难度：0.7

  解析

四、解答题（共70分）

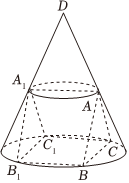• 21．如图，一个圆锥挖掉一个内接正三棱柱ABC-A₁B₁C₁（棱柱各顶点均在圆锥侧面或底面上），若棱柱侧面BCC₁B₁落在圆锥底面上．已知正三棱柱底面边长为

  2

  3

  ，高为2．
  （1）求挖掉的正三棱柱ABC-A₁B₁C₁的体积；
  （2）求该几何体的表面积．
  组卷：67引用：7难度：0.4

  解析

• 22．已知O为坐标原点，对于函数f（x）=asinx+bcosx,称向量

  OM

  =

  （

  a

  ,

  b

  ）

  为函数f（x）的伴随向量，同时称函数f（x）为向量

  OM

  的伴随函数．
  （1）设函数

  g

  （

  x

  ）

  =

  sin

  （

  x

  +

  2

  π

  3

  ）

  +

  cos

  （

  π

  2

  -

  x

  ）

  ，试求g（x）的伴随向量

  OM

  ；
  （2）记向量

  ON

  =

  （

  1

  ，

  3

  ）

  的伴随函数为f（x），求当

  f

  （

  x

  ）

  =

  6

  5

  且

  x

  ∈

  （

  -

  π

  3

  ，

  π

  6

  ）

  时，sinx的值；
  （3）已知将（2）中的函数y=f（x）的图象上各点的纵坐标不变，横坐标缩短到原来的

  1

  2

  倍，再把整个图象向右平移

  π

  3

  个单位长度得到h（x）的图象，若存在

  x

  ∈

  （

  0

  ，

  π

  2

  ）

  ，使4h（x）+1=2•[a-h²（x）]成立，求a的取值范围．
  组卷：163引用：7难度：0.5

  解析