2023-2024学年湖北省恩施州来凤实验中学八年级（上）第一次月考数学试卷
发布：2024/9/22 10:0:8
一、选择题（共12小题，每小题3分，满分36分）
-
1．下列各组中的两个图形属于全等形的是（ ）
组卷：450引用：13难度：0.8 -
2．如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A=60°，∠B=40°，则∠ECD等于（ ）组卷：4700引用：60难度：0.9 -
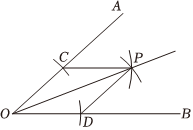3．如图，用尺规作已知角平分线，其根据是构造两个三角形全等，它所用到的判别方法是（ ）组卷：967引用：31难度：0.9 -
4．如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=（ ）组卷：6087引用：31难度：0.7 -
5．下列说法中，正确的个数是（ ）
①三角形的中线、角平分线、高都是线段；②三角形的三条角平分线、三条中线、三条高都在三角形内部；③直角三角形只有一条高；④三角形的三条角平分线、三条中线、三条高分别交于一点．组卷：10066引用：29难度：0.8 -
6．若一个多边形的内角和与它的外角和相等，则这个多边形是（ ）
组卷：3980引用：66难度：0.9 -
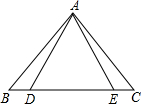7．如图，△ABE≌△ACD，∠B=50°，∠AEC=120°，则∠DAC的度数等于（ ）组卷：662引用：24难度：0.9 -
8．下列各组线段能组成一个三角形的是（ ）
组卷：146引用：6难度：0.8
三、解答题（共8小题，满分72分）
-
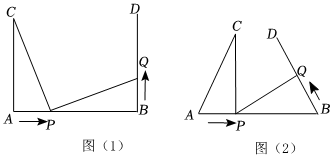23．如图（1），AB=9cm,AC⊥AB，BD⊥AB垂足分别为A、B，AC=7cm.点P在线段AB上以2cm/s的速度由点A向点B运动，同时点Q在射线BD上运动．它们运动的时间为t（s）（当点P运动结束时，点Q运动随之结束）．
（1）若点Q的运动速度与点P的运动速度相等，当t=1时，△ACP与△BPQ是否全等，请说明理由；
（2）如图（2），若“AC⊥AB，BD⊥AB”改为“∠CAB=∠DBA”，点Q的运动速度为x cm/s,其它条件不变，当点P，Q运动到何处时有△ACP与△BPQ全等，求出相应的x的值．组卷：168引用：4难度：0.5 -
24．（1）如图（1），在平面直角坐标系中，将直角三角形的直角顶点放在点P（6，6）处，两直角边与坐标轴交于点A和点B．求OA+OB的值；
（2）将直角三角形绕点P逆时针旋转，如图（2）两直角边与坐标轴交于点A和点B，求OA-OB的值；
（3）在图（2）的基础上，由点P引一条射线PG，如图（3），过点A作AM⊥PG，过点B作BN⊥PG，垂足分别为M，N，猜想AM，BN，MN之间的数量关系，并说明理由．
组卷：79引用：3难度：0.1
