2022-2023学年广东省东莞实验中学高一（下）月考数学试卷（5月份）

一、单项选择题（本大题共8小题，每小题5分，共40分，每小题只有一个正确选项）

• 1．若i为虚数单位，复数z满足z（1+i）=|3+4i|，则z的虚部为（　　）

  A． 5 2 i

  B． 5 2

  C． - 5 2 i

  D． - 5 2
  组卷：336引用：6难度：0.8

  解析

• 2．已知向量

  a

  =（2，3），

  b

  =（x,2），则“

  a

  与

  b

  的夹角为锐角”是“x＞-3”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：279引用：11难度：0.7

  解析

• 3．下表是足球世界杯连续八届的进球总数：
  

  年份	1994	1998	2002	2006	2010	2014	2018	2022
  进球总数	141	171	161	147	145	171	169	172

  则进球总数的第40百分位数是（　　）

  A．147

  B．154

  C．161

  D．165
  组卷：205引用：4难度：0.8

  解析

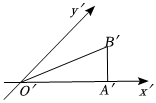• 4．若△OAB的直观图如图所示，∠B'A'O'=

  π

  2

  ，B'A'=2，则顶点B到x轴的距离是（　　）

  A．2

  B．4

  C． 2

  D． 4 2
  组卷：284引用：8难度：0.8

  解析

• 5．将一个大圆锥截去一个小圆锥得到圆台，圆台的上、下底面圆的半径之比为1：3，若大圆锥的高为15，则圆台的高为（　　）

  A．10

  B． 15 4

  C． 45 4

  D．5
  组卷：58引用：1难度：0.7

  解析

• 6．△ABC中，角A，B，C的对边分别是a,b,c,已知b=c,a²=2b²（1-sinA），则A=（　　）

  A． 3 π 4

  B． π 3

  C． π 4

  D． π 6
  组卷：10580引用：39难度：0.7

  解析

• 7．如图，四面体ABCD中，AB，BC，BD两两垂直，BC=BD=2，点E是CD的中点，若直线AB与平面ACD所成角的正切值为

  2

  4

  ，则点B到平面ACD的距离为（　　）

  A． 2 3

  B． 2 3

  C． 2 2 3

  D． 4 3
  组卷：155引用：8难度：0.4

  解析

四、解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤）

• 21．锐角三角形△ABC的内角A，B，C的对边分别为a,b,c,若

  c

  -

  acos

  B

  =

  3

  3

  bsin

  A

  ．
  （1）求A；
  （2）求sinB+sinC的取值范围．
  组卷：69引用：1难度：0.5

  解析

• 22．如图1，在长方形ABCD中，AB=2，AD=1，E为CD的中点，以AE为折痕，把△DAE折起为△D′AE，且平面D′AE⊥平面ABCE（如图2）．
  （1）求证：AD′⊥BE；
  （2）求四棱锥D′-ABCE的体积；
  （3）在棱D′E上是否存在一点P，使得D′B∥平面PAC，若存在，求出点P的位置，不存在，说明理由．
  
  组卷：217引用：17难度：0.5

  解析