2022-2023学年安徽省马鞍山七中九年级（上）期中数学试卷

一.选择题（本题共10小题，每小题4分，演分40分）

• 1．抛物线y=x²-4x+7的顶点坐标为（　　）

  A．（-2，3）

  B．（-2，-3）

  C．（2，-3）

  D．（2，3）
  组卷：460引用：8难度：0.9

  解析

• 2．已知（x₁，y₁），（x₂，y₂），（x₃，y₃）是反比例函数

  y

  =

  -

  4

  x

  的图象上三点，且x₁＜x₂＜0＜x₃，则y₁，y₂，y₃的大小关系是（　　）

  A．y1＜0＜y2＜y3

  B．y1＞y2＞0＞y3

  C．y1＜y2＜0＜y3

  D．y3＜0＜y1＜y2
  组卷：48引用：2难度：0.7

  解析

• 3．已知正方形ABCD，E是CD的中点，P是BC边上的一点，下列条件中不能推出△ABP与△ECP相似的是（　　）

  A．∠APB=∠EPC	B．AB•PC=EC•BP
  C．P是BC的中点	D．BP：BC=2：3
  组卷：43引用：6难度：0.6

  解析

• 4．已知a,b,c均为正数，且

  a

  b

  +

  c

  =

  b

  c

  +

  a

  =

  c

  a

  +

  b

  =k,则下列四个点中，在正比例函数y=kx图象上的点的坐标是（　　）

  A．（1， 1 2 ）

  B．（1，2）

  C．（1，- 1 2 ）

  D．（1，-1）
  组卷：259引用：4难度：0.5

  解析

• 5．二次函数y=ax²+bx+c的图象如图所示，则一次函数y=bx+a与反比例函数y=

  a

  +

  b

  +

  c

  x

  在同一坐标内的图象大致为（　　）

  A．

  B．

  C．

  D．
  组卷：498引用：8难度：0.7

  解析

• 6．某公司在甲、乙两地同时销售某种品牌的汽车．已知在甲、乙两地的销售利润y（万元）与销售量x（辆）之间分别满足：

  y

  1

  =

  -

  x

  2

  +

  10

  x

  ，y₂=2x,若该公司在甲、乙两地共销售15辆该品牌的汽车，则能获得的最大利润为（　　）

  A．30万元

  B．38万元

  C．46万元

  D．48万元
  组卷：66引用：3难度：0.5

  解析

• 7．下列图形中，阴影部分面积最大的是（　　）

  A．

  B．

  C．

  D．
  组卷：3621引用：86难度：0.9

  解析

七.（本题满分12分）

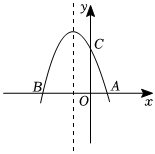• 22．如图，抛物线y=ax²-2x+c与x轴交于A（1，0），B（-3，0）两点．
  （1）求该抛物线的解析式；
  （2）设抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由；
  （3）在第二象限内的抛物线上是否存在一点P，使△PBC的面积最大？若存在，求出点P的坐标及△PBC的面积最大值；若不存在，请说明理由．
  组卷：86引用：3难度：0.5

  解析

八.（本题满分14分）

• 23．在△ABC中，P为边AB上一点．
  
  （1）如图1．若∠ACP=∠B，求证：AC²=AP•AB．
  （2）若M为CP的中点，AC=2．
  ①如图2，若∠PBM=∠ACP，AB=3，求BP的长．
  ②如图3，若∠ABC=45°，∠A=∠BMP=60°，直接写出BP的长．
  组卷：153引用：3难度：0.1

  解析