2023-2024学年北京市首都师大附中昌平学校高二(上)期中数学试卷
发布:2024/9/23 12:0:8
一、选择题(每题4分)
-
1.设A(3,2,1),B(1,0,5),则AB的中点M的坐标为( )
组卷:525引用:4难度:0.8 -
2.直线
的倾斜角为( )x+y-3=0组卷:130引用:3难度:0.9 -
3.已知以点A(2,-3)为圆心,半径长等于5的圆O,则点M(5,-7)与圆O的位置关系是( )
组卷:726引用:10难度:0.9 -
4.已知向量
=(-3,2,5),a=(1,x,-1),且b⊥a,则x的值为( )b组卷:351引用:21难度:0.8 -
5.点(1,1)到直线x-y-1=0的距离是( )
组卷:578引用:2难度:0.8 -
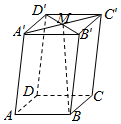 6.如图,在平行六面体ABCD-A′B′C′D′中,若,AB=a,AD=b,则AA′=c=( )BM组卷:289引用:4难度:0.7
6.如图,在平行六面体ABCD-A′B′C′D′中,若,AB=a,AD=b,则AA′=c=( )BM组卷:289引用:4难度:0.7 -
7.平面α的法向量为(3,1,-2),平面β的法向量为(-1,1,k),若α⊥β,则k=( )
组卷:129引用:4难度:0.7
三、解答题(17-19题13分,20题14分,21题15分,22题12分)
-
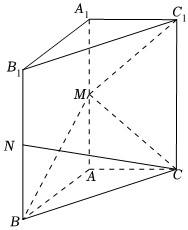 21.如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,M、N分别是AA1,BB1的中点,AB=AA1=2,AC=1.
21.如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,M、N分别是AA1,BB1的中点,AB=AA1=2,AC=1.
(Ⅰ)求证:C1M⊥CN;
(Ⅱ)求直线CN与平面BCM所成角的正弦值;
(Ⅲ)求平面BCM与平面ABB1A1所成角的余弦值.组卷:184引用:3难度:0.4 -
22.在xOy平面上,我们把与定点F1(-a,0)、F2(a,0)(a>0)距离之积等于a2的动点的轨迹称为伯努利双纽线,F1、F2为该曲线的两个焦点.已知曲线C:(x2+y2)2=9(x2-y2)是一条伯努利双纽线.
(1)求曲线C的焦点F1、F2的坐标;
(2)判断曲线C上是否存在两个不同的点A、B(异于坐标原点O),使得以AB为直径的圆过坐标原点O.如果存在,求点A、B坐标;如果不存在,请说明理由.组卷:70引用:3难度:0.5


