当前位置：试卷中心 > 试卷详情

2022-2023学年安徽省合肥一中高一（下）期中数学试卷

发布：2024/7/20 8:0:8

一、单项选择题（共8小题，每题5分，满分40分）．

1．若复数z=a²-4+（a-2）i为纯虚数，则实数a的值为（　　）
A．2 B．2或-2 C．-2 D．-4
组卷：218引用：9难度：0.7
解析
2．在△ABC中，内角A，B，C的对边分别为a,b,c,且满足c=2acosB，则△ABC的形状是（　　）
A．等腰三角形
B．直角三角形
C．等腰直角三角形
D．等腰三角形或直角三角形
组卷：1161引用：21难度：0.9
解析
3．某圆锥的侧面展开图是半径为3，圆心角为120°的扇形，则该圆锥的体积为（　　）
A．
4
5
π
B．
4
5
3
π
C．
2
2
π
D．
2
2
3
π
组卷：529引用：6难度：0.9
解析
4．△ABC中，三个内角A，B，C的对边分别为a,b,c.已知
A
=
π
4
，
a
=
2
，
b
=
3
，则B的大小为（　　）
A．
π
6
B．
π
3
C．
π
6
或
5
π
6
D．
π
3
或
2
π
3
组卷：133引用：5难度：0.7
解析
5．设点P为△ABC内一点．且2
PA
+2
PB
+
PC
=0，则S_△ABP：S_△ABC=（　　）
A．
1
5
B．
2
5
C．
1
4
D．
1
3
组卷：1650引用：7难度：0.6
解析
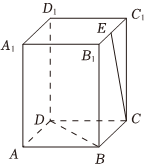6．如图，在长方体ABCD-A₁B₁C₁D₁中，已知AB=BC=2，AA₁=5，E为B₁C₁的中点，则异面直线BD与CE所成角的余弦值为（　　）
A．
5
10
B．
34
34
C．
13
26
D．
13
13
组卷：479引用：8难度：0.7
解析
7．在《九章算术》中，底面为矩形的棱台被称为“刍童”．已知棱台ABCD-A′B′C′D′是一个侧棱相等、高为1的“刍童”，其中AB=2A′B′=2，
BC
=
2
B
′
C
′
=
2
3
，则该“刍童”外接球的表面积为（　　）
A．20π B．
20
3
π
C．
20
5
3
π
D．
5
5
π
组卷：206引用：5难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（共6小题，其中第17题10分，其余各题12分，满分70分）

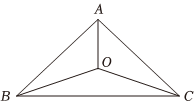21．合肥一中云上农舍有三处苗圃，分别位于图中△ABC的三个顶点，已知
AB
=
AC
=
20
2
m
，BC=40m.为了解决三个苗圃的灌溉问题，现要在△ABC区域内（不包括边界）且与B，C等距的一点O处建立一个蓄水池，并铺设管道OA、OB、OC．
（1）设∠OBC=θ，记铺设的管道总长度为ym,请将y表示为θ的函数；
（2）当管道总长取最小值时，求θ的值．
组卷：27引用：3难度：0.5
解析
22．数学史上著名的波尔约-格维也纳定理：任意两个面积相等的多边形，它们可以通过相互拼接得到．它由法卡斯•波尔约（FarksBolyai）和保罗•格维也纳（PaulGerwien）两位数学家分别在1833年和1835年给出证明．现在我们来尝试用平面图形拼接空间图形，使它们的全面积都与原平面图形的面积相等：（1）给出两块相同的正三角形纸片（如图1、图2），其中图1，沿正三角形三边中点连线折起，可拼得一个正三棱锥；图2，正三角形三个角上剪出三个相同的四边形（阴影部分），其较长的一组邻边边长为三角形边长的
1
4
，有一组对角为直角，余下部分按虚线折起，可成一个缺上底的正三棱柱，而剪出的三个相同的四边形恰好拼成这个正三棱锥的上底．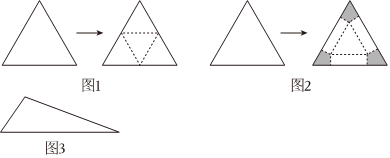

（1）试比较图1与图2剪拼的正三棱锥与正三棱柱的体积的大小；
（2）如果给出的是一块任意三角形的纸片（如图3），要求剪拼成一个直三棱柱模型，使它的全面积与给出的三角形的面积相等．请仿照图2设计剪拼方案，用虚线标示在图3中，并作简要说明．
组卷：18引用：2难度：0.5
解析