2022-2023学年吉林省长春市二道区八年级（下）期末数学试卷

一、选择题（本大题共8小题，每小题0分，共24分）

• 1．64的平方根是（　　）

  A．8

  B．-8

  C．±8

  D．32
  组卷：134引用：5难度：0.9

  解析

• 2．下列运算正确的是（　　）

  A．（ab）3=ab3

  B．a8÷a2=a4

  C．（a2）3=a5

  D．a2•a3=a5
  组卷：145引用：4难度：0.5

  解析

• 3．下列命题：
  （1）同位角相等，两直线平行；
  （2）多边形的内角和等于180°；
  （3）三角形的外角和等于360°；
  （4）平行于同一条直线的两条直线互相平行．其中真命题的个数为（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：28引用：2难度：0.5

  解析

• 4．若x²-kx+9是完全平方式，则k的值是（　　）

  A．±3

  B．±6

  C．3

  D．6
  组卷：1283引用：13难度：0.7

  解析

• 5．若△ABC中∠A、∠B、∠C的对边分别是a,b,c,下列条件不能说明△ABC是直角三角形的是（　　）

  A．b2=（a+c）（a-c）	B．a：b：c=1： 3 ：2
  C．∠C=∠A-∠B	D．∠A：∠B：∠C=3：4：5
  组卷：1264引用：17难度：0.5

  解析

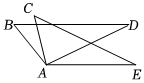• 6．如图，已知AB=AC，AD=AE，欲证△ABD≌△ACE，不可补充的条件是（　　）

  A．BD=CE

  B．∠D=∠E

  C．∠BAD=∠CAE

  D．∠BAC=∠DAE
  组卷：263引用：5难度：0.7

  解析

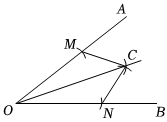• 7．小明同学在用直尺和圆规作一个角的平分线，具体过程是这样的：
  已知：∠AOB．
  求作：∠AOB的平分线．
  作法：第一步：如图，以点O为圆心，适当长为半径画弧交OA于点M，交OB于点N．
  第二步：分别以点M、N为圆心，大于

  1

  2

  的长为半径画弧，两弧在∠AOB的内部相交于点C．
  第三步：画射线OC．
  射线OC就是所要求作的∠AOB的平分线．
  下列关于小明同学作法的理由，叙述正确的是（　　）

  A．由SAS可得△OCM≌△OCN，进而可证∠AOC=∠BOC

  B．由SSS可得△OCM≌△OCN，进而可证∠AOC=∠BOC

  C．由ASA可得△OCM≌△OCN，进而可证∠AOC=∠BOC

  D．由“等边对等角”可得∠AOC=∠BOC
  组卷：19引用：2难度：0.5

  解析

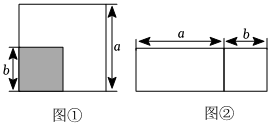• 8．如图①，从边长为a的正方形中剪去一个边长为b的小正方形，然后将剩余分剪拼成一个长方形（如图②），则上述操作所能验证的公式是（　　）

  A．a2+ab=a（a+b）	B．（a-b）2=a2-2ab+b2
  C．（a+b）2=a2+2ab+b2	D．a2-b2=（a+b）（a-b）
  组卷：1088引用：9难度：0.8

  解析

三、解答题（本大题共10小题，共78分）

• 23．阅读材料：
  若x满足（9-x）（x-4）=4，求（9-x）²+（x-4）²的值．
  解：设9-x=a,x-4=b,则（9-x）（x-4）=ab=4，
  ∴a+b=（9-x）+（x-4）=5，
  ∴（9-x）²+（x-4）²=a²+b²=（a+b）²-2ab=5²-2×4=17．
  类比应用：
  （1）若（3-x）（x-2）=-1，求（3-x）²+（x-2）²的值．
  （2）若（n-2022）²+（2023-n）²=10，则（n-2022）（2023-n）的值为

  ．
  （3）已知正方形ABCD的边长为a,点P和点R分别是边AB和CD上的点，且AP=4，CR=2，分别以BP和DR为边长作正方形PBEF和正方形DMNR．若图中阴影部分长方形的面积是4，则正方形PBEF和正方形DMNR的面积和为

  ．
  组卷：71引用：1难度：0.5

  解析

• 24．如图，在Rt△ABC中，∠ACB=90°，AB=15cm,BC=9cm,过点A作射线AD∥BC．点P从点B出发，以3cm/s的速度沿BA向终点A运动：点Q从点A出发，以a cm/s的速度沿射线AD运动．点P、Q同时出发，当点P到达点A时，点P、Q同时停止运动．连结PC、PQ，设运动时间为t（s）．
  ​
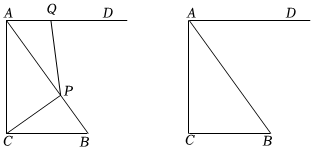
  （1）线段AP=

  cm（用含t的代数式表示）．
  （2）求AC的长．
  （3）当△APQ与△BCP全等时，
  ①若点P、Q的移动速度相同，求t的值．
  ②若点P、Q的移动速度不同，求a的值．
  组卷：69引用：2难度：0.5

  解析