2022-2023学年湖北省十堰市高三（上）月考数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小颗给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合

  A

  =

  {

  x

  |

  y

  =

  4

  x

  -

  x

  2

  }

  ，B={x|1-x＞0}，则A∪B=（　　）

  A．{x|0≤x＜1}

  B．{x|x≤4}

  C．{x|1＜x≤4}

  D．{x|x≥0}
  组卷：162引用：6难度：0.9

  解析

• 2．设i是虚数单位，复数z₁=2-i,z₂=1+3i,则z₁•z₂=（　　）

  A．-1-5i

  B．-1+5i

  C．5-5i

  D．5+5i
  组卷：3引用：4难度：0.9

  解析

• 3．“

  sinα

  =

  2

  3

  ”是“

  cos

  2

  α

  =

  1

  9

  ”的（　　）

  A．充要条件	B．充分不必要条件
  C．必要不充分条件	D．既不充分也不必要条件
  组卷：144引用：5难度：0.7

  解析

• 4．已知直线y=3x+1与双曲线C：

  y

  2

  a

  2

  -

  x

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  相交，且有且仅有1个交点，则双曲线C的离心率是（　　）

  A．10

  B． 10

  C． 10 3

  D． 10 3
  组卷：50引用：3难度：0.7

  解析

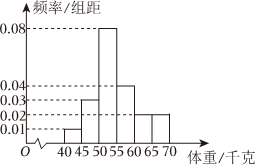• 5．《中国居民膳食指南（2022）》数据显示，6岁至17岁儿童青少年超重肥胖率高达19.0%．为了解某地中学生的体重情况，某机构从该地中学生中随机抽取100名学生，测量他们的体重（单位：千克），根据测量数据，按[40，45），[45，50），[50，55），[55，60），[60，65）分成六组，得到的频率分布直方图如图所示．根据调查的数据，估计该地中学生体重的中位数是（　　）

  A．50

  B．52.25

  C．53.75

  D．55
  组卷：204引用：4难度：0.8

  解析

• 6．已知

  a

  ＞

  1

  4

  ，

  b

  ＞

  1

  2

  ，且2a+b=2，则

  1

  4

  a

  -

  1

  +

  1

  2

  b

  -

  1

  的最小值是（　　）

  A．1

  B． 4 3

  C．2

  D． 5 2
  组卷：471引用：3难度：0.7

  解析

• 7．如图，等边三角形ABC的边长为3，DE⊥AB分别交AB，AC于D，E两点，且AD=1，将△ADE沿DE折起（点A与P重合），使得平面PDE⊥平面BCED，则折叠后的异面直线PB，CE所成角的正弦值为（　　）

  A． 3 2

  B． 6 3

  C． 5 5

  D． 2 5 5
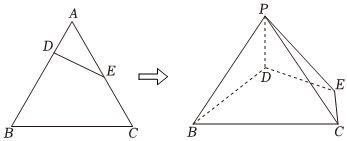  组卷：62引用：5难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的右焦点为F，P在椭圆C上，|PF|的最大值与最小值分别是6和2．
  （1）求椭圆C的标准方程．
  （2）若椭圆C的左顶点为A，过点F的直线l与椭圆C交于B，D（异于点A）两点，直线AB，AD分别与直线x=8交于M，N两点，试问∠MFN是否为定值？若是，求出该定值；若不是，请说明理由．
  组卷：41引用：5难度：0.5

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  （

  x

  -

  m

  ）

  e

  x

  -

  1

  m

  x

  2

  +

  nx

  ，且曲线y=f（x）在x=0处的切线为y=-2．
  （1）求m,n的值和f（x）的单调区间；
  （2）若f（x₁）=f（x₂）=f（x₃）（x₁＜x₂＜x₃），证明：x₁+x₂＞0．
  组卷：119引用：5难度：0.5

  解析