2022-2023学年河南省南阳一中高一(下)第二次月考数学试卷
发布:2024/6/14 8:0:9
一、选择题(其中1-8题为单选题;9-12题为多选题;每小题5分共60分)
-
1.-885°化成2kπ+α(0≤α≤2π,k∈Z)的形式是( )
组卷:312引用:7难度:0.9 -
2.化简:(1)
,(2)AB+BC+CA,(3)AB-AC+BD-CD,(4)FQ+QP+EF-EM,结果为零向量的个数是( )OA-OB+AB组卷:188引用:1难度:0.8 -
3.函数
的图象大致为( )f(x)=12x2-xsinx组卷:174引用:5难度:0.7 -
4.已知O是△ABC内一点,且满足
,则O点一定是△ABC的( )OA•OB=OB•OC=OC•OA组卷:155引用:6难度:0.9 -
5.已知灯塔A在海洋观测站C的北偏东40°的方向上,A,C两点间的距离为5海里.某时刻货船B在海洋观测站C的南偏东80°的方向上,此时B,C两点间的距离为8海里,该时刻货船B与灯塔A间的距离为( )
组卷:23引用:2难度:0.6 -
6.已知
,a=(sinα)sinα,b=(cosα)sinα,c=(tanα)sinα,则( )α∈(0,π6)组卷:203引用:3难度:0.7 -
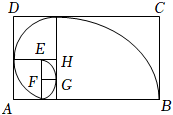 7.斐波那契螺旋线被誉为自然界最完美的“黄金螺旋”,它的画法是:以斐波那契数1,1,2,3,5,8,…为边长比例的正方形拼成矩形,然后在每个正方形中画一个圆心角为90°的圆弧,这些圆弧所连起来的弧线就是斐波那契螺旋线.如图,矩形ABCD是由若干符合上述特点的正方形拼接而成,其中|AB|=16,则图中的斐波那契螺旋线的长度为( )组卷:147引用:7难度:0.8
7.斐波那契螺旋线被誉为自然界最完美的“黄金螺旋”,它的画法是:以斐波那契数1,1,2,3,5,8,…为边长比例的正方形拼成矩形,然后在每个正方形中画一个圆心角为90°的圆弧,这些圆弧所连起来的弧线就是斐波那契螺旋线.如图,矩形ABCD是由若干符合上述特点的正方形拼接而成,其中|AB|=16,则图中的斐波那契螺旋线的长度为( )组卷:147引用:7难度:0.8
三、解答题(共70分)
-
 21.如图所示,在△ABC中,已知点D在边BC上,且∠DAC=90°,cos∠DAB=,AB=6.223
21.如图所示,在△ABC中,已知点D在边BC上,且∠DAC=90°,cos∠DAB=,AB=6.223
(1)若sinC=,求线段BC的长;33
(2)若点E是BC的中点,AE=,求线段AC的长.17组卷:32引用:2难度:0.5 -
22.已知函数f(x)=4sin(ωx+
)(ω>0)在[π3,π]上单调递减.π6
(1)求ω的最大值;
(2)若f(x)的图象关于点(,0)中心对称,且f(x)在[-3π2,m]上的值域为[-2,4],求m的取值范围.9π20组卷:457引用:8难度:0.4


